參數假設檢驗(parametric hypothesis test )簡稱假設檢驗,是數理統計學中根據一定假設條件由樣本推斷總體的一種方法。
其基本原理是先對總體的特徵作出某種假設,然後通過抽樣研究的統計推理,對此假設應該被拒絕還是接受作出推斷。
基本介紹
- 中文名:參數假設檢驗
- 外文名:parametric hypothesis test
- 分類:數學 統計學
- 時間:20世紀初
- 提出者:K.Pearson
- 檢驗:顯著性水平
簡介
基本思想
步驟
意義
套用
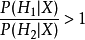

參數假設檢驗(parametric hypothesis test )簡稱假設檢驗,是數理統計學中根據一定假設條件由樣本推斷總體的一種方法。
其基本原理是先對總體的特徵作出某種假設,然後通過抽樣研究的統計推理,對此假設應該被拒絕還是接受作出推斷。
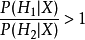
參數假設檢驗(parametric hypothesis test )簡稱假設檢驗,是數理統計學中根據一定假設條件由樣本推斷總體的一種方法。其基本原理是先對總體的特徵作出某種假設,然後通過...
假設檢驗是推斷統計中的一項重要內容。用SAS、SPSS等專業統計軟體進行假設檢驗,在假設檢驗中常見到P值( P-Value,Probability,Pr),P值是進行檢驗決策的另一個依據...
參數檢驗(parameter test)全稱參數假設檢驗,是指對參數平均值、方差進行的統計檢驗。參數檢驗是推斷統計的重要組成部分。當總體分布已知(如總體為常態分配),根據樣本...
相似檢驗(similar test)是功效函式在參數空間的特定子集上保持常數的檢驗。功效函式亦稱勢函式,假設檢驗中的一種機率,是指採用某檢驗時否定原假設的機率。...
P值是用來判定假設檢驗結果的一個參數,也可以根據不同的分布使用分布的拒絕域進行比較。由R·A·Fisher首先提出。P值(P value)就是當原假設為真時,比所得到的...
推斷統計包括兩方面的內容:總體參數估計和假設檢驗。推斷統計總體參數估計 當研究中從樣本獲得一組數據後,如何通過這組信息,對總體特徵進行估計,也就是如何從局部...
1 基本信息 2 參數估計 3 假設檢驗 4 自變數的選擇 5 解決方案 多重線性回歸基本信息 編輯 多重線性回歸的數學模型為:式...
推論統計(inferential statistics)是藉助抽樣調查,從局部推斷總體,以對不肯定的事物做出決策的一種統計。有總體參數估計與假設檢驗兩種。前者以一次性抽樣實驗為依據,...
本書介紹了工科研究生“數理統計”課程的基本內容,包括:預備知識、抽樣分析、參數估計、假設檢驗、方差分析、正交實驗設計、回歸分析和多元統計分析初步等,同時還介紹...
主要內容為事件與機率,隨機變數及其分布,數字特徵,極限定理,抽樣分布,參數估計,假設檢驗以及方差分析和回歸分析等。《機率統計習題精解》內容精練,編排合理,每一章節...
推論統計就是運用樣本的統計值來推斷總體的參數值。因此,如何抽取樣本,樣本的可靠程度,分析可靠程度的保證及進行假設檢驗,都是推論統計需要研究的問題。...
內容包括隨機事件及其機率、一維隨機變數及其分布、多維隨機變數及其分布、隨機變數的數字特徵及極限定理、數理統計的基本概念與抽樣分布、參數估計、假設檢驗和方差分析...
本書是數理統計學的專業基礎課教材。內容包括緒論、抽樣分布、點估計、區間估計、假設檢驗、非參數檢驗和分布的檢驗、Bayes方法和統計判決理論等七章,各章都配備了...
《高等學校教材:套用數理統計》內容主要涉及數理統計的基本概念、參數估計、假設檢驗、回歸分析、方差分析、正交試驗、多元統計分析等。《高等學校教材:套用數理統計》...
方法分為連續型隨機變數的統計方法與離散型隨機變數的統計方法兩章,為便於教學,在本版教材中“總體參數的統計方法”改為“總體參數估計”與“總體參數假設檢驗”兩...
全書共分十章,包括機率論的基本概念、條件機率與獨立性、隨機變數及基分布、隨機變數的數字特徵、大數定律與中心極限定理、參數估計、假設檢驗、ExceI在機率統計中的...
全書共有10章和1個附錄,第1章介紹了機率論與矩陣代數的預備知識;第2章給出數理統計的基本概念;第3章和第4章是參數估計和假設檢驗,在大學相關內容的基礎上作了...
隨機變數及其分布,隨機向量及其分布,隨機變數的函式及其數值模擬,隨機變數的數字特徵,大數定律與中心極限定理,樣本與抽樣分布,參數估計,假設檢驗,機率統計的MATLAB命令...
主要內容包括:機率論的基本概念、隨機變數及其機率分布、數字特徵、大數定律與中心極限定理、統計量及其機率分布、參數估計和假設檢驗、回歸分析、方差分析、馬爾科夫鏈...
第六章 參數假設檢驗第一節 假設檢驗的基本概念第二節 總體均值的假設檢驗第三節 總體成數的假設檢驗第四節 總體方差的假設檢驗第五節 用SPSS作假設檢驗...
《研究生系列教材:套用數理統計》比較系統地介紹了數理統計的基本概念、原理和方法。全書分為6章,內容包括數理統計的基本概念、參數估計、假設檢驗、方差分析和正交...
本書共分7章,主要包括:隨機事件及其機率、一維隨機變數及其分布、多維隨機變數及其分布、隨機變數的數字特徵、數理統計的基本概念、參數估計和假設檢驗。本書是為適應...
《綜合統計分析》是2002年蘭州大學出版社出版的圖書,作者是李元章。本書詳細地闡述了參數估計的綜合統計分析、假設檢驗的綜合統計分析、相關係數的綜合統計分析以及離散...
《統計學:統計數據分析理論與方法》內容由原來的十章增加到十三章,增加了參數估計、假設檢驗、方差分析和面板數據分析,在內容上涵蓋描述統計、推斷統計、多元統計以...
