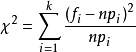卡方檢驗

卡方檢驗

卡方檢驗是用途非常廣的一種假設檢驗方法，它在分類資料統計推斷中的套用，包括：兩個率或兩個構成比比較的卡方檢驗；多個率或多個構成比比較的卡方檢驗以及分類資料的相關分析等。

基本介紹

  • 中文名：卡方檢驗
  • 外文名：chi-square test ；X,2-test
  • 種類：假設檢驗方法
  • 套用：分類資料統計推斷
  • 作用：資料分析
  • 定義：觀測值與理論值之間的偏離程度
基本原理,步驟,檢驗方法,資料檢驗,代碼實現,

基本原理

卡方檢驗就是統計樣本的實際觀測值與理論推斷值之間的偏離程度，實際觀測值與理論推斷值之間的偏離程度就決定卡方值的大小，如果卡方值越大，二者偏差程度越大；反之，二者偏差越小；若兩個值完全相等時，卡方值就為0，表明理論值完全符合。
注意：卡方檢驗針對分類變數。

步驟

（1）提出原假設：
H0：總體X的分布函式為F(x).
如果總體分布為離散型，則假設具體為
H0：總體X的分布律為P{X=xi}=pi， i=1，2，...
（2）將總體X的取值範圍分成k個互不相交的小區間A1，A2，A3，…，Ak，如可取
A1=（a0，a1]，A2=(a1，a2]，...，Ak=(ak-1,ak)，
其中a0可取-∞，ak可取+∞，區間的劃分視具體情況而定，但要使每個小區間所含的樣本值個數不小於5，而區間個數k不要太大也不要太小。
（3）把落入第i個小區間的Ai的樣本值的個數記作fi，成為組頻數（真實值），所有組頻數之和f1+f2+...+fk等於樣本容量n。
（4）當H0為真時，根據所假設的總體理論分布，可算出總體X的值落入第i 個小區間Ai的機率pi，於是，npi就是落入第i個小區間Ai的樣本值的理論頻數（理論值）。
（5）當H0為真時，n次試驗中樣本值落入第i個小區間Ai的頻率fi/n與機率pi應很接近，當H0不真時，則fi/n與pi相差很大。基於這種思想，皮爾遜引進如下檢驗統計量
，在0假設成立的情況下服從自由度為k-1的卡方分布。

檢驗方法

獨立樣本四格表
自由度為1
假設有兩個分類變數X和Y，它們的值域分別為{x1, x2}和{y1, y2}，其樣本頻數列聯表為
y1
y2
總計
x1
a
b
a+b
x2
c
d
c+d
總計
a+c
b+d
a+b+c+d
若要推斷的論述為H1：“X與Y有關係”，可以利用獨立性檢驗來考察兩個變數是否有關係，並且能較精確地給出這種判斷的可靠程度。具體的做法是，由表中的數據算出檢驗統計量
的值。
的值越大，說明“X與Y有關係”成立的可能性越大。
0.50
0.40
0.25
0.15
0.10
k
0.455
0.708
1.323
2.072
2.706
0.05
0.025
0.010
0.005
0.001
k
3.841
5.024
6.635
7.879
10.828
當表中數據a，b，c，d都不小於5時，可以查閱下表來確定結論“X與Y有關係”的可信程度：
例如，當“X與Y有關係”的
的值為6.109，根據表格，因為5.024<6.109<6.635，所以“X與Y有關係”成立的機率在1-0.01到1-0.025之間。
男
女
化妝
15（55）
95（55）
110
不化妝
85（45）
5（45）
90
100
100
200
如果性別和化妝與否沒有關係，四個格子應該是括弧里的數（期望值，用極大似然估計55=100*110/200，其中110/200可理解為化妝的機率，乘以男人數100，得到男人化妝機率的似然估計），這和實際值（括弧外的數）有差距，理論和實際的差距說明這不是隨機的組合。
套用擬合度公式
=
129.3>10.828
顯著相關，作此推論成立的機率p>0.999,即99.9%。
註：獨立四格表的擬合度公式可以寫成n(ad-bc)^2/(a+b)(c+d)(a+c)(b+d)
總結：獨立四格表資料檢驗
四格表資料的卡方檢驗用於進行兩個率或兩個構成比的比較。
1. 專用公式：
若四格表資料四個格子的頻數分別為a，b，c，d，則四格表資料卡方檢驗的卡方值=n(ad-bc)^2/(a+b)(c+d)(a+c)(b+d)，（或者使用擬合度公式）
自由度v=（行數-1）（列數-1）=1
2. 套用條件：
要求樣本含量應大於40且每個格子中的理論頻數不應小於5。當樣本含量大於40但有1=<理論頻數<5時，卡方值需要校正，當樣本含量小於40或理論頻數小於1時只能用確切機率法計算機率。

資料檢驗

（自由度df=(C-1)(R-1)）
行×列表資料的卡方檢驗用於多個率或多個構成比的比較。
1. 專用公式：
r行c列表資料卡方檢驗的卡方值=n[(A11/n1n1+A12/n1n2+...+Arc/nrnc)-1]
2. 套用條件：
要求每個格子中的理論頻數T均大於5或1<T<5的格子數不超過總格子數的1/5。當有T<1或1<T<5的格子較多時，可採用並行並列、刪行刪列、增大樣本含量的辦法使其符合行×列表資料卡方檢驗的套用條件。而多個率的兩兩比較可採用行X列表分割的辦法。
列聯表資料檢驗
同一組對象，觀察每一個個體對兩種分類方法的表現，結果構成雙向交叉排列的統計表就是列聯表。
1. R*C 列聯表的卡方檢驗：
R*C 列聯表的卡方檢驗用於R*C列聯表的相關分析，卡方值的計算和檢驗過程與行×列表資料的卡方檢驗相同。
2. 2*2列聯表的卡方檢驗：
2*2列聯表的卡方檢驗又稱配對記數資料或配對四格表資料的卡方檢驗，根據卡方值計算公式的不同，可以達到不同的目的。當用一般四格表的卡方檢驗計算時，卡方值=n（ad-bc)^2/[(a+b)(c+d)(a+c)(b+d)]，此時用於進行配對四格表的相關分析，如考察兩種檢驗方法的結果有無關係；當卡方值=（|b-c|-1）2/(b+c)時，此時卡方檢驗用來進行四格表的差異檢驗，如考察兩種檢驗方法的檢出率有無差別。
列聯表卡方檢驗套用中的注意事項同R*C表的卡方檢驗相同。

代碼實現

在分類資料統計分析中我們常會遇到這樣的資料，如兩組大白鼠在不同致癌劑作用下的發癌率如下表，問兩組發癌率有無差別？
處理
發癌數
未發癌數
合計
發癌率%
甲組
52
19
71
73.24
乙組
39
3
42
92.86
合計
91
22
113
80.53
這是表中最基本的數據，因此上表資料又被稱之為四格表資料。卡方檢驗的統計量是卡方值，它是每個格子實際頻數A與理論頻數T差值平方與理論頻數之比的累計和。每個格子中的理論頻數T是在假定兩組的發癌率相等（均等於兩組合計的發癌率）的情況下計算出來的，如第一行第一列的理論頻數為71*(91/113)=57.18，故卡方值越大，說明實際頻數與理論頻數的差別越明顯，兩組發癌率不同的可能性越大。
卡方檢驗要求：最好是大樣本數據。一般每個個案最好出現一次，四分之一的個案至少出現五次。如果數據不符合要求，就要套用校正卡方。
利用統計學軟體分析結果如下：
data kafang;
input row column number @@;
cards;
1 1 52
1 2 19
2 1 39
2 2 3
;
run;
proc freq;
tables row*column/chisq;
weight number;
run;
統計量
自由度
值
機率
卡方
1
6.4777
0.0109（顯著）
似然比卡方
1
7.3101
0.0069
連續校正卡方
1
5.2868
0.0215
Mantel-Haenszel 卡方
1
6.4203
0.0113
Phi 係數
-0.2394
列聯繫數
0.2328
Cramer 的 V
-0.2394

相關詞條

熱門詞條

聯絡我們