勒貝格逐項積分定理(Lebesgue term by termintegration theorem)級數形式的積分極限定理之一。
基本介紹
- 中文名：勒貝格逐項積分定理
- 外文名：Lebesgue term by termintegration theorem
- 適用領域：積分極限定理
定義
若{fn(二)}為可測集E上的非負可測函式列，則
勒貝格逐項積分定理
這從逐項積分角度，反映了勒貝格積分比黎曼積分運算更靈活.
勒貝格逐項積分定理
相關詞條
- 勒貝格逐項積分定理
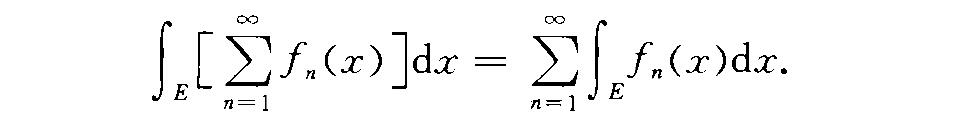
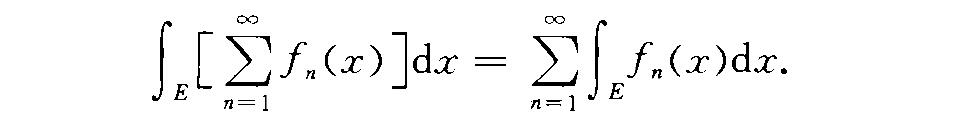
勒貝格逐項積分定理(Lebesgue term by termintegration theorem)級數形式的積分極限定理之一。定義若{fn(二)}為可測集E上的非負可測函式列，則這從逐項積分角度，反映了勒貝格積分比黎...
- 勒貝格積分
唯一的延伸。這個積分正好就是勒貝格積分。這個結果可以被廣泛化來建立關於局部緊空間的拉東測度的積分理論。2004年尼古拉·布爾巴基就是使用了這個方法。套用 值得指出的是許多拓撲向量空間（比如希爾伯特空間或者巴拿赫空間）中的定理以及其中...
- 勒貝格定理
在數學分析中，勒貝格定理，或稱黎曼-勒貝格定理是一個傅立葉分析方面的結果。這個定理有兩種形式，分別是關於周期函式（傅立葉理論中關於傅立葉級數的方面）和關於在一般實數域R上定義的函式（傅立葉變換的方面）。在任一種形式下，...
- 積分公式
勒貝格積分 黎曼－斯蒂爾傑斯積分 數值積分 公式匯總 不定積分 不定積分的積分公式主要有如下幾類：含ax+b的積分、含√（a+bx）的積分、含有x^2±α^2的積分、含有ax^2+b（a>0）的積分、含有√（a²+x^2）（a>0）的積分...
- 測度論(研究一般集合上的測度和積分的理論)
定理的形成 縱觀勒貝格積分和勒貝格－斯蒂爾傑斯積分理論，不難發現它們都有三個基本要素。第一，一個基本空間（即n維歐幾里得空間 R ）以及這個空間的某些子集構成的集類即L（勒貝格）可測集或某L－S（勒貝格-斯蒂爾傑斯）可測集全體，...
- 積分(數學術語)
上的最大值和最小值，那么：其中的 在黎曼積分中表示區間 的長度，在勒貝格積分中表示 的測度。種類 黎曼積分 達布積分 勒貝格積分 黎曼-斯蒂爾吉斯積分 數值積分 相關知識 微積分基本定理 不定積分 定積分 積分符號 積分表 ...
- 黎曼-勒貝格定理
黎曼-勒貝格定理(Riemann-Lebesgue's Theory)提出了所有函式的傅立葉展開均收斂於其自身，黎曼-勒貝格定理在信號處理、傅立葉分析上有重要的套用。Riemann-Lebesgue定理指出，任何一個函式f的Fourier常數趨向於0；這個命題在某種意義下，即使...
- 勒貝格控制收斂定理
勒貝格控制收斂定理是更廣泛的法圖-勒貝格定理（Fatou–Lebesgue theorem）的特例。以下是一個引用法圖引理的證明。由於 是 逐點收斂的極限，因此對其仍然有 （於是 ）。同理，對任意的 有： 根據法圖引理， 因此，由勒貝格積分的...
- 勒貝格可積函式
勒貝格可積函式是指其勒貝格積分為有限數的函式，簡稱(L)可積函式。在(L)測度有限的集上，有界可測函式都是(L)可積函式。簡介 勒貝格可積函式是指其勒貝格積分為有限數的函式，簡稱(L)可積函式。若f(x)是可測集E⊂Rⁿ上的...
- 勒貝格測度
。然後定義集合A為勒貝格可測的，如果對於所有集合 ，都有： 這些勒貝格可測的集合形成了一個σ代數。勒貝格測度定義為λ(A) = λ(A)對於任何勒貝格可測的集合A。根據維塔利定理，存在實數 的一個勒貝格不可測的子集。如果A是 的...
- 勒貝格函式
勒貝格函式 勒貝格函式（Lebesgue function）是1993年公布的數學名詞。公布時間 1993年，經全國科學技術名詞審定委員會審定發布。出處 《數學名詞》第一版。
- 勒貝格有界收斂定理
定理敘述 設 為一個測度空間， 是一個實值的可測函式列。如果 逐點收斂於一個函式 ，並存在一個勒貝格可積的函式 ，使得對每個 ，任意 ，都有：則：也是勒貝格可積的，；其中的函式 一般取為正值函式。函式列 的逐點收斂和 的...
- 歐氏空間上的勒貝格積分(修訂版)
《歐氏空間上的勒貝格積分（修訂版）》是2018年世界圖書出版公司出版的著作，作者是Frank、Jones 。內容簡介 The treatment ofintegration developed by the French mathematician Henri Lebesgue （1875-1944） almost a century ago has ...
- 抽象積分
對於積分存在和可積兩個概念也做類似定義，當(Ω，F，μ)是完備測度空間時，抽象積分的性質與勒貝格積分的性質基本相同，也有關於積分收斂性的三大定理(列維定理、法圖引理、勒貝格控制收斂定理)。也可以引進平均收斂等概念，並且與幾乎處處...
- 歐氏空間上的勒貝格積分
Rn的Fubini定理；Gamma函式；Lp空間；抽象測度的乘積；卷積；Rn+上的傅立葉變換；單變數傅立葉積分；微分；R上函式的微分。讀者對象 《歐氏空間上的勒貝格積分(修訂版)(英文版)》適用於數學專業的學生、老師和相關的科研人員。
- Lebesgue測度與積分(2017年東南大學出版社出版的圖書)
該書根據信息與計算科學專業實際情況——教學課時少的特點，精簡傳統實變函式論中部分抽象內容，對某些抽象概念、定理等內容都舉例說明,從而降低該課程難度，減輕學生負擔，提高學生學習積極性.我們主要介紹Lebesgue(勒貝格)測度與Lebesgue積分...
- 勒貝格分解定理
勒貝格分解定理(Lebesgue decomposition theorem)是關於σ有限廣義測度分解為絕對連續部分和奇異部分之和的重要定理，是有界變差函式的勒貝格分解定理的推廣。設(Ω，F，μ)是σ有限測度空間，若γ是(Ω，F)上的σ有限測度，則γ可分解為...
- 實分析(機械工業出版社出版圖書)
3 Fubini定理 3 1定理的敘述與證明 3 2 Fubi¨ni定理的套用 4+ 傅立葉反演公式 5習題 6問題 第3章微分與積分 1積分的微分 1 1 哈代一李特爾伍德極大函式 1 2勒貝格微分定理 2好的核與恆同逼近 第4章希爾伯特空間簡介 ...
- 可測函式
設f是定義在可測集E上的實函式。如果對每一個實數，集E[f>a]恆可測（勒貝格可測），則稱f是定義在 E上的（勒貝格）可測函式。定理 設f是定義在可測集E上的實函式，下列任一個條件都是在E上（勒貝格）可測的充要條件：（...
- 戚民駒
在二十多年的教學生涯中先後在中文核心期刊、統計源期刊、省級期刊上共發表了二十餘篇論文，在實函式理論（特別是積分學理論）方面有較深入的研究，先後給出並證明了一維（2001年）、N-維（2009年）勒貝格可測函式的本性定理，即任一...
