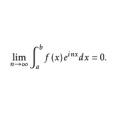黎曼-勒貝格定理

黎曼-勒貝格定理(Riemann-Lebesgue's Theory)提出了所有函式的傅立葉展開均收斂於其自身，黎曼-勒貝格定理在信號處理、傅立葉分析上有重要的套用。Riemann-Lebesgue定理指出，任何一個函式f的Fourier常數趨向於0；這個命題在某種意義下，即使對連續函式而言，也不能再改進了。因為，假如(Χ_n)是任意一個正的遞降數列但具有極限為0，我們可以選取一個趨向無窮大的整數序列n_k適合於k>Χ_nk。級數∑kcos n_kθ為一致收斂，所以它是一個連續函式的Fourier級數而當n=n_k時a_n=k>Χ_n。

基本介紹

• 中文名：黎曼-勒貝格定理
• 外文名：Riemann-Lebesgue's Theory
• 所屬學科：數學
• 內容：函式的傅立葉展開均收斂於其自身
• 套用：信號處理、傅立葉分析

基本介紹

定理 設，則當時

定理的證明

證明 這裡不妨假設f(x)具有周期b-a： f(x+b-a)=f(x)。對於正數ε，有全連續函式φ(x)適合

置：

就得到

將δ趨近於0，我們得到，因為ε是任意的。

顯然地，我們也不妨假設b-a=2π.假設

那么

而

定理證明完畢。

相關結論

系1 設是的係數，則。

當f(x)∈L(a，b)時，稱為f在區間[a，b]上的平均連續模數，假如f(x)∈C(a，b)，那么稱

為f(x)在[a，b]上的連續模，當（C和α都是常數）時，記著

假如f(x)不是常數，那么α≤1。

系2 假如f(x+2π)≡f(x)，，那么的傅立葉係數都是O(n)；當f∈Lip 1時na_n和nb_n都是o(1)。

事實上，，當f∈Lip 1時，是一全連續函式，從而也是傅立葉級數，=o(1)。

假如是一個有界變差的函式，，那么

後者表示f(x)在[-π，π]上的全變差．這個結果，從下式

立刻明白，但是不能改進為．事實上，我們可舉例

來說明，另一方面，黎茲舉例說明有界變差的連續函式f(x)≡f(x+2π)的係數c_n也未必是．

哈代(G.H.Hardy)於1916年在美國數學會通報(T.A.M.S.17)上證明：當O<a<1，ab >1（b：正整數）時，函式屬於，這裡

由於，所以並不含有。