基本介紹
- 中文名:剩餘設計
- 外文名:residual design
- 所屬學科:數學
- 所屬問題:組合學(組合設計理論)
- 簡介:由對稱設計導出的BIBD
基本介紹














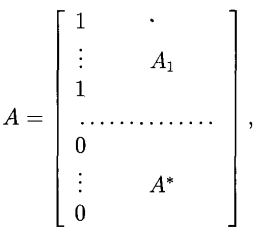







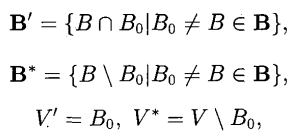

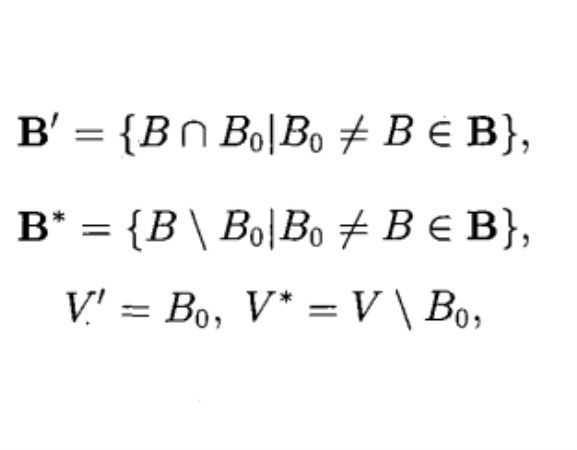






















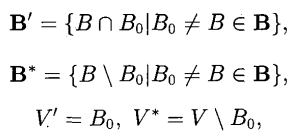

剩餘設計(residual design)是一種由對稱設計導出的平衡不完全區組設計,具體的構作方法如下:設(X,B)是一個(v,k,λ)-SBIBD,取定一個區組B0,對其餘的區組B,記B′=B\B0,且B′={B′|B...
當一個BIBD設計的參數為(v-k,v-1,k,k-λ,λ)時,稱為擬剩餘設計。若一個擬剩餘設計是某個對稱設計的剩餘設計,則稱該擬剩餘設計是可嵌入的,利用康納-霍爾定理可以證明某些BIBD設計不存在。基本介紹 定義1 若v,k與λ滿足...
剩餘區組設計 剩餘區組設計(residual block design)是1993年公布的數學名詞。公布時間 1993年,經全國科學技術名詞審定委員會審定發布。出處 《數學名詞》第一版。
《長三角鄉村家庭剩餘空間公共使用的設計類型研究》是依託同濟大學,由婁永琪擔任項目負責人的青年科學基金項目。中文摘要 長三角地區高速城市化導致城鄉社會、經濟結構的快速轉型,農村剩餘勞動力向城市轉移產生了大量的鄉村家庭剩餘空間;同時...
residual design)。上面給出的構作法。其實就是取定B₀∈B。令 則(V',B')便是D的導出設計,便是D的剩餘設計。若v,k與λ滿足條件 ,設D*為一個B(k-λ,λ;v-k),則稱D*為一個擬剩餘設計(quasi residual design)。
由來 零浪費設計,本質就是儘可能少地剩餘碎布料。如果大家都這么做,就是消除每年成千上萬噸垃圾的好方法。時裝業內人士都清楚,有15%~20%的面料其實最終都被丟進了垃圾桶,因為比起費心思再利用這些剩餘面料,直接丟掉要少花錢得多...
剩餘電流動作斷路器具有防止人觸電功能,按照IEC標準人體在通過電流30mA的情況將會發生明顯器官的損傷和心臟纖維顫抖,時間超過1秒將會有電擊致死的危險,因此在低壓配電系統中要求安裝剩餘電流斷路器(RCD),與線路上的電壓無關。在TN-C系統...
額定剩餘動作電流是製造廠對剩餘電流動作保護裝置規定的剩餘動作電流值,在該電流值時,剩餘電流保護裝置應在規定的條件下動作。簡介 額定剩餘動作電流是製造廠對剩餘電流動作保護裝置規定的剩餘動作電流值,在該電流值時,剩餘電流保護裝置應...
1.2 平衡不完全區組設計 1.3 成對平衡設計與可分組設計 1.4 正交拉丁方與橫截設計 1.5 t-設計 1.6 註記 第2章 對稱設計理論基礎 2.1 對稱PBD設計 2.2 對稱設計的關聯矩陣 2.3 擬剩餘設計 2.4 Bnmk—Ryser—Chowla...
《剩餘公主第一季》(朝鮮語:잉여공주)是韓國tvN自2014年8月7日起播出的木曜連續劇。分集劇情 簡介 《剩餘公主第一季》講述來到首爾和就業生住在一起的人魚公主在100天內找到真愛,變成真正人類的故事。本劇原定14集,後來因...
剩餘電壓繞組 剩餘電壓繞組(residual voltage winding)是1998年公布的電氣工程名詞。公布時間 1998年,經全國科學技術名詞審定委員會審定發布。出處 《電氣工程名詞》第一版。
計畫的剩餘 計畫的剩餘,見“經濟剩餘”。
《二維循環填充和具有單純剩餘的可分解填充研究》是依託蘇州大學,由殷劍興擔任項目負責人的面上項目。項目摘要 填充問題是當代組合設計理論中一個基本的研究課題,為Hanani、Mills、Mullin等眾多著名組合學專家所關注。本項目研究兩類重要的...
上述各系統在2012年9月之前的核電站設計中均被不同程度的提及和套用,但是,也存在著一些缺陷和不足。《一種核電站能動與非能動結合的堆芯剩餘熱量排出系統》通過合理的改進和系統的最佳化,克服了上述各系統在2012年9月之前技術中所存在...
契約維護成本主要取決於集群信用網路、集群信息共享網路、集群合作剩餘分配、集群內競爭機制、契約條款等。集群信用網路和集群信息共享網路建設越好,集群內競爭機制設定越科學,集群合作剩餘分配方案越合理,契約條款設計越全面,則集群企業會更...
最初設計這種試驗用作比較不同材料的一種手段。但這些試驗已被廣泛用於確定設計許用值。相比之下,通常認為衝擊損傷後的拉伸剩餘強度並不像其他幾何特徵那么重要,例如,緊固件孔和缺口更加危險。充壓的機身是個例外情況,必須證實當它含有...
1.3 對稱PBD設計 1.4 t-設計 習題 第二章 拉丁方與正交序列 2.1 橫截設計 2.2 拉丁方與正交序列 2.3 Euler猜想的否定 習題 第三章 幾類對稱設計 3.1 對稱,PBD設計 3.2 對稱BIB的關聯矩陣 3.3 擬剩餘設計 3.4 對稱...
如果滿足強度要求,即認為設計完畢;當強度不夠.或設計人員認為剩餘強度太大時則修改設計。再估算、修改主要截面尺寸,然後再進行強度校核,一般可能重複1~2次。計算分析均以工程梁理論為基礎,並對結構中受力特性不符合工程梁基本假設的...
康納-霍爾定理(Connor-Hall theorem)是關於擬剩餘設計的嵌人定理 。該定理斷言:又一2的擬剩餘設計都是剩餘設計,即都是可嵌人的.關於可嵌人的情況,除了 =2外,因又一1時的擬剩餘設計是仿射平面,從而也是可嵌人的.對 >3,...
devise e 設計 ; 發明 ; 策劃 ; 想出 devise a proposal 設計一份提案 heir by devise [法] 遺囑贈與繼承人 ; 翻譯 advertising devise 廣告設計 general devise 概括性財產轉讓 ; 翻譯 residuary devise 剩餘不動產遺贈 devise a...
舉例而言,一塊地,適用於工業還是商業,或者,一塊居住用地,是用於低強度開發的豪宅,還是高強度開發的商品房,取決於兩者誰能創造最大的淨剩餘(利潤)。在增量規劃里,這塊屬於政府。只要設計一個制度,比如招拍掛,馬上我們就可以確定...
