導出設計(derived design)是一種重要的設計,指由對稱設計導出的平衡不完全區組設計。
基本介紹
- 中文名:導出設計
- 外文名:derived design
- 所屬學科:數學(組合學)
- 簡介:由對稱設計導出的BIB設計
基本介紹







相關分析














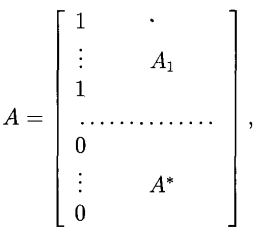



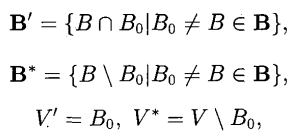


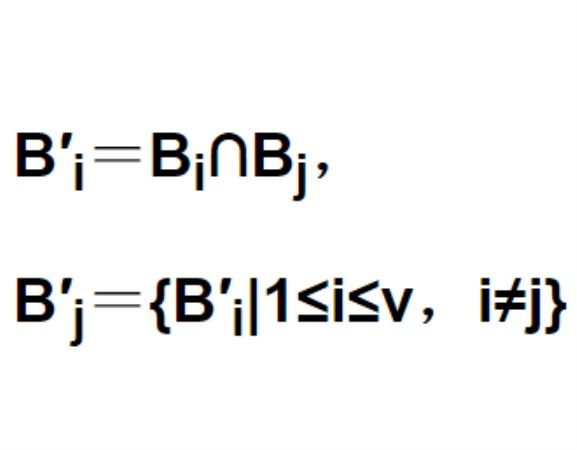
導出設計(derived design)是一種重要的設計,指由對稱設計導出的平衡不完全區組設計。

























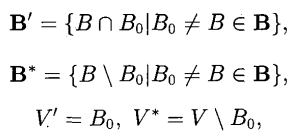


導出設計(derived design)是一種重要的設計,指由對稱設計導出的平衡不完全區組設計。...
輸出設計指依據系統分析和系統綜合階段 所確定的有關輸出報表和檔案的格式及其內 容,設計出符合使用者要求的系統輸出信息 的詳細內容和格式。包括輸出的具體數據和 ...
輸入輸出設計是管理信息系統與用戶的界面,一般而言,輸入輸出 設計對於系統開發人員並不重要,但對用戶來說,卻顯得尤為重要。...
“導出”式教學作為一種產出導向、互教互學為基本特徵的教學方法,即由學習“成果”為固著點組織教學,讓學生在蒐集、探究、展示、反饋的過程中建構知識、啟迪思維...
《設計生成》是2008年8月1日甘肅人民美術出版社出版的圖書。... 《設計生成》是2008年8月1日甘肅人民美術出版社出版的圖書。書名 設計生成 ISBN 9787805887005 ...
剩餘設計(residual design)是一種由對稱設計導出的平衡不完全區組設計,具體的構作方法如下:設(X,B)是一個(v,k,λ)-SBIBD,取定一個區組B0,對其餘的區組B...
互動設計(英文Interaction Design, 縮寫IXD),是定義、設計人造系統的行為的設計領域,它定義了兩個或多個互動的個體之間交流的內容和結構,使之互相配合,共同達成某種...
稅收信息系統輸出設計是稅收電算信息系統為用戶提供輸出信息的內容、方式、格式以及使用什麼介質的設計。輸出是稅收電算信息系統與用戶的重要接口,系統是否方便實用,...
三、計量要求的導出1.將產品性能和生產的技術要求表示為技術指標參數要求或產品性能指標的形式表示出來,把設計工藝檔案或圖紙上的技術要求表示為表示為技術參數,把...
《建築生成設計》 是東南大學出版社出版的圖書, ISBN是 9787564134020... 《建築生成設計--基於複雜系統的建築設計計算機生成方法研究(精)》基於複雜系統模型,通過...
您可以在輸出選項卡中指定一個輸出表的名稱、位置和邏輯庫。參考資料 1. 丁革建. BD排版語言與資料庫輸出表格設計[J]. 計算機技術與發展, 1996(6):44-45....
詳細設計,是軟體工程中軟體開發的一個步驟,就是對概要設計的一個細化,就是詳細設計每個模組實現算法,所需的局部結構。在詳細設計階段,主要是通過需求分析的結果,...
只要您的客戶設計好輸出樣稿,不論何時,檔案通過線上輸出在彈指間便可傳輸到您的手中。便於管理客戶資料線上輸出擁有專門記錄輸出中心與客戶間檔案傳遞的資料庫,實現...
有三種基本形式: (1) 物質技術輸出,如向別國提供成套設備、主機和重要零部件等。這是技術製品的轉移,技術供應方能獲得較多的外匯收入。(2) 設計技術輸出,如向...
(三)設計的國際化視角。選題策劃階段,還應該把選題內容和輸出對象國讀者的文化背景、閱讀習慣、閱讀心理、審美標準等結合起來,設計出符合他們審美要求的裝幀形式和...
導出限值是指可以產生與基本限值相應的電場、磁場和功率通量密度的值。由於基本量很難測出,所以大多數檔案給出了電場、磁場和功率密度的導出(參考)限值。當暴露...
本書可作為印刷、包裝、藝術設計、編輯出版等相關專業高職高專教材,也可作為相關領域企業、單位的職工教育學校、函大等教材,並可供相關行業人員入門學習參考。 [1]...
業務流程設計是指根據市場需求與企業要求調整企業流程,包括設計、分析和最佳化流程。設計階段主要包括兩項任務:其一,透視現有流程質量;其二,根據當前市場需求調整現有...
EasyCode軟體輔助設計生成系統是一款基於.NET底層框架的重新最佳化設計的工具。它真正實現了面向對象的設計,而不是面向資料庫設計,可以直接生成專業級別WinForm和Asp.Net...
導出脈衝是指羅蘭C接收的射頻脈衝和它的反射頻脈衝延遲相加後得出的脈衝。其包絡線相當於原射頻脈衝包絡的微分,它在離脈衝起始點的特定位置有一個零點,該射頻脈衝...
《Processing創意編程——生成設計|數據可視化|聲音可視化》2019年10月清華大學出版社出版的圖書,作者是任遠。 ...
三次設計是在20世紀70年代由日本質量管理專家田口玄一提出的,包括系統設計(第一次設計)、參數設計(第二次設計)和容差設計(第三次設計)。它是一種最佳化設計,主要...
參數設計是三次設計法里的二次設計,是在系統設計之後進行。參數設計的基本思想是通過選擇系統中所有參數(包括原材料、零件、元件等)從而儘量減少外部、內部和產品間...
不受時間限制:只要客戶設計好輸出樣稿,不論何時,檔案通過線上輸出便可。便於管理客戶資料: 線上輸出擁有專門記錄輸出中心與客戶間檔案傳遞的資料庫,實現強大的客戶...
品牌輸出—具體體現為為企業提供品牌市場調研、規劃、產品研發、生產、包裝、設計、生產、營運、供應鏈管理、市場推廣、行銷管理、品牌打造、實施,企業管理服務等整套...
計算機輔助設計是指利用計算機及其圖形設備幫助設計人員進行設計工作,但存在著需要存儲和處理的圖形和數據量極大的問題。而以互動式技術組建的互動式CAD/CAM(計算機...
設計質量是指根據使用者的使用目的、經濟狀況及企業內部條件確定所需設計的質量等級或質量水平。它反映著設計目標的完善程度,表現為各種規格和標準。...
一鍵生成是一款可自動生成ppt、海報、名片等的傻瓜式工具app。由武漢示界港科技有限公司開發,採用雲端排版技術,提供了多種圖片、字型、模板等設計元素。用戶輸入文字...
數據轉換程式就是為數據轉換而設計的程式。數據轉換程式不僅可作輸入排序使用,而且還有列印、複製功能,具有標準例行程的功能。這種程式也稱實用程式(Utility Program)。...
