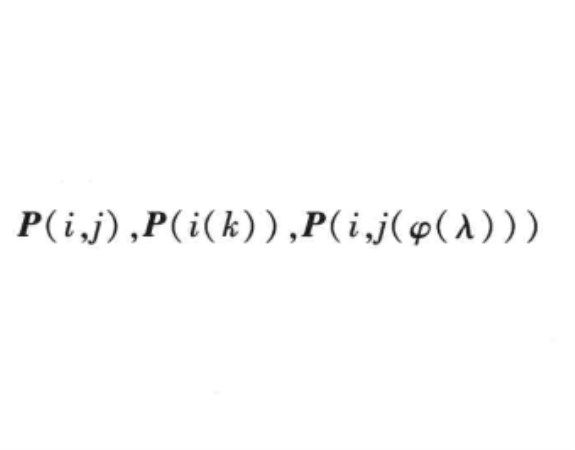單位矩陣經過一次λ-矩陣的初等變換得到的矩陣稱為初等λ-矩陣，共三類：P(i，j)，P(i(k))，P(i，j(φ(λ)))，它們是可逆的，且(P(i，j))=P(i，j)，(P(i(k)))=P(i(1/k))，(P(i，j(φ(λ))))=(P(i，j(φ(-λ))))。對一個s×n的λ-矩陣A(λ)作一次初等變換就相當於在A(λ)的左邊乘上相應s×s的初等矩陣；對A(λ)做一次初等列變換就相當於A(λ)在的右邊乘上相應的n×n的初等矩陣。
基本介紹
- 中文名：初等λ矩陣
- 外文名：elementary λ-matrices
- 所屬學科：數學
- 簡介：三種形狀簡單且經常使用的λ矩陣
- 性質：初等λ矩陣都是可逆的
基本介紹,相關介紹,
基本介紹
初等λ矩陣(elementary λ-matrices)是一類簡單的λ矩陣。指三種形狀簡單且經常使用的λ矩陣，數域P上的n階λ矩陣中，下列的三種矩陣稱為初等λ矩陣：
1.P(j(d))=E+(d-1)Ejj，d∈P，且d≠0 (j=1，2，…，n)；
2.P(i，j(b(λ)))=E+b(λ)Eij(i，j=1，2，…，n，且i≠j)；
3.P(i，j)=E-Eii-Ejj+Eij+Eji(i，j=1，2，…，n，且i≠j)，
其中E為n階單位矩陣，Eij是矩陣單位，b(λ)是λ的多項式。初等λ矩陣都是可逆的，且
P(i(d))=P(i(d))，
P(i，j(b(λ)))=P(i，j(-b(λ)))，
P(i，j)=P(i，j)。
定理 矩陣A(λ)是可逆的充分必要條件是它可以表成一些初等矩陣的乘積。
推論 兩個s×n的λ-矩陣A(λ)與B(λ)等價的充分必要條件為，有一個s×s可逆矩陣P(λ)與一個n×n可逆矩陣Q(λ)，使B(λ)=P(λ)A(λ)Q(λ)。
相關介紹
λ矩陣的初等變換是與初等λ矩陣密切相關的λ矩陣的三種變換的統稱，下列的三種變換稱為數域P上的λ矩陣的初等變換：
1.用數域P中非零數d乘矩陣的第j行(列)；
2.把矩陣的第j行(列)的b(λ)倍加到第i行(列)；
3.互換矩陣的第i行(列)與第j行(列)。
設A(λ)是數域P上的m×n的λ矩陣，對A(λ)的行(列)施行變換1，相當於用m(n)階初等矩陣P(j(d))左(右)乘A(λ)；施行變換2，相當於用m(n)階初等矩陣P(i，j(b(λ)))左(右)乘A(λ)；施行變換3，相當於用m(n)階初等矩陣P(i，j)左(右)乘A(λ)。
說明：
1. λ-矩陣的初等變換與數字矩陣的初等變換的差別:前兩類變換是一樣的,但第三類初等變換是將某一行(列)的φ(λ)倍加到另一行(列)上，不再是一個常數倍。
第二類變換之所以仍然是乘以非零的常數c，而不是乘以一個非零的多項式，是為了使初等變換能夠可逆。
2.與數字矩陣一樣,把單位矩陣E經過一次初等變換得到的λ-矩陣稱為λ-初等矩陣；並且，λ-初等矩陣都是可逆的。
3.對一個s×n的λ-矩陣A(λ)作一次初等行變換就相當於對A(λ)左乘一個相應的s×s初等矩陣；對A(λ)作一次初等列變換就相當於對A(λ)右乘一個相應的n×n初等矩陣。
4.矩陣A(λ)與B(λ)等價的充分必要條件是存在λ-初等矩陣
,使得
如果A(λ)與B(λ)等價,那么|A(λ)|與|B(λ)|只相差一個非零常數，但是，與數字矩陣的情形不同，兩個秩相同的λ-矩陣A(λ)與B(λ)卻不一定等價，例如: 
和
的秩都為2，但是|A(λ)|=1≠λ=|B(λ)]，即|A(λ)|與|B(λ)|不相差一個非零常數，從而不等價。
