列秩

在線性代數中，一個矩陣A的列秩是A的線性獨立的縱列的極大數目。類似地，行秩是A的線性獨立的橫行的極大數目。

矩陣的列秩和行秩總是相等的，因此它們可以簡單地稱作矩陣A的秩。通常表示為r(A)，rk(A)或rank A。

基本介紹

• 中文名：列秩
• 外文名：column rank
• 定義：線性獨立的縱列的極大數目
• 表示：r(A)，rk(A)或rank A
• 套用學科：線性代數
• 相關術語：行秩

行秩列秩相等

矩陣的行秩與列秩相等，是線性代數基本定理的重要組成部分. 其基本證明思路是，矩陣可以看作線性映射的變換矩陣，列秩為像空間的維度，行秩為非零原像空間的維度，因此列秩與行秩相等，即像空間的維度與非零原像空間的維度相等（這裡的非零原像空間是指約去了零空間後的商空間：原像空間）。這從矩陣的奇異值分解就可以看出來。

給出這一結果的兩種證明. 第一個證明是簡短的，僅用到向量的線性組合的基本性質. 第二個證明利用了正交性. 第一個證明利用了列空間的基, 第二個證明利用了行向量空間的基. 第一個證明適用於定義在標量域上的矩陣，第二個證明適用於內積空間。二者都適用於實或復的歐氏空間，也都易於修改去證明當A是線性變換的情形。

證明一

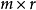令A是一個的矩陣，其列秩為 r。因此矩陣A的列空間的維度是r。 令是A的列空間的一組基，構成矩陣C的列向量，並使得A的每個列向量是C的r個列向量的線性組合. 由矩陣乘法的定義，存在一個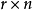矩陣R， 使得 A=CR。(A的(i,j)元素是與 R的第 j個列向量的點積。)

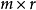
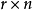
現在，由於A=CR,A的每個行向量是R的行向量的線性組合，這意味著A的行向量空間被包含於R的行向量空間之中. 因此A的行秩 ≤R的行秩. 但R僅有r行, 所以R的行秩 ≤r=A的列秩. 這就證明了A的行秩 ≤A的列秩.

把上述證明過程中的“行”與“列”交換，利用對偶性質同樣可證A的列秩 ≤ A的行秩。更簡單的方法是考慮 A的轉置矩陣，則A的列秩 =的行秩 ≤的列秩 = A的行秩. 這證明了A的列秩等於A的行秩，證畢。

證明二

令A是一個m×n矩陣. 定義rk(A)為A的列秩，A為A的共軛轉置或稱施密特轉置. 首先可知AAx= 0若且唯若Ax= 0.

• AAx= 0 ⇒xAAx= 0 ⇒(Ax)(Ax)= 0 ⇒ ‖Ax‖= 0 ⇒ Ax = 0,
  

其中‖·‖是歐氏範數。這說明A的零空間與AA的零空間相同。由秩－零化度定理，可得rk(A) = rk(AA)。AA的每一個列向量是A的列向量的線性組合。所以AA的列空間是A的列空間的子空間，從而rk(AA) ≤ rk(A)。 即: rk(A) = rk(AA) ≤ rk(A)。 套用這一結果於A可或得不等式: since (A)=A，可寫作rk(A) ≤ rk((A)) = rk(A)，這證明了rk(A) = rk(A)，證畢。

可替代定義

向量組的秩

向量組的秩：在一個m維線性空間E中，一個向量組的秩表示的是其生成的子空間的維度。考慮m×n矩陣 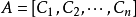，將A的秩定義為向量組F的秩，則可以看到如此定義的A的秩就是矩陣A的線性無關列向量的極大數目，即A的列空間的維度（列空間是由A的縱列生成的F的子空間）。因為列秩和行秩是相等的，我們也可以定義A的秩為A的行空間的維度。

線性映射

考慮線性映射：

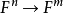對於每個矩陣A，都是一個線性映射，同時，對每個的 線性映射f，都存在矩陣A使得。也就是說，映射

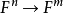
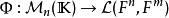
是一個同構映射。所以一個矩陣A的秩還可定義為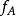的像的維度（像與核的討論參見線性映射）。矩陣A稱為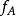的變換矩陣。這個定義的好處是適用於任何線性映射而不需要指定矩陣，因為每個線性映射有且僅有一個矩陣與其對應。秩還可以定義為n減f的核的維度；秩-零化度定理聲稱它等於f的像的維度。

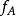
性質

我們假定A是在域F上的m×n矩陣並描述了上述線性映射。

• m×n矩陣的秩不大於m或n的一個非負整數，表示為 rk(A) ≤ min(m,n)。有儘可能大的秩的矩陣被稱為有滿秩；類似的，否則矩陣是秩不足（或稱為“欠秩”）的。
  
• 只有零矩陣有秩0
  
• A的秩最大為min(m,n)
  
• f是單射，若且唯若A有秩n（在這種情況下，我們稱A有“列滿秩”）。
  
• f是滿射，若且唯若A有秩m（在這種情況下，我們稱A有“行滿秩”）。
  
• 在方塊矩陣A(就是m=n)的情況下，則A是可逆的，若且唯若A有秩n（也就是A有滿秩）。
  
• 如果B是任何n×k矩陣，則AB的秩最大為A的秩和B的秩的小者。即：
  

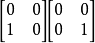
• A的秩等於r，若且唯若存在一個可逆m×m矩陣X和一個可逆的n×n矩陣Y使得
  

這裡的I_r指示r×r單位矩陣。

• 西爾維斯特不等式: 如果A是一個m×n的矩陣且B是n×k的, 則
  

• 矩陣的秩加上矩陣的零化度等於矩陣的縱列數（這就是秩-零化度定理）。
  
• 如果A是實數上的矩陣，那么A的秩和它對應格拉姆矩陣的秩相等。
  
• 如果A是複數上的矩陣且A* 表示A的共軛轉置(i.e.,A的伴隨), 則
  

計算

計算矩陣A的秩的最容易的方式是高斯消去法，即利用矩陣的初等變換生成一個行階梯形矩陣，由於矩陣的初等變換不改變矩陣的秩，因此A的行梯陣形式有同A一樣的秩。經過初等變換的矩陣的非零行的數目就是原矩陣的秩。

例如考慮4 × 4矩陣

我們看到第2縱列是第1縱列的兩倍，而第4縱列等於第1和第3縱列的總和。第1和第3縱列是線性無關的，所以A的秩是2。這可以用高斯算法驗證。它生成下列A的行梯陣形式:

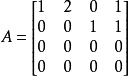
它有兩個非零的橫行。

在套用在計算機上的浮點數的時候，基本高斯消去（LU分解）可能是不穩定的，應當使用秩啟示（revealing）分解。一個有效的替代者是奇異值分解（SVD），但還有更少代價的選擇，比如有支點（pivoting）的QR分解，它也比高斯消去在數值上更強壯。秩的數值判定要求對一個值比如來自SVD的一個奇異值是否為零的依據，實際選擇依賴於矩陣和套用二者。

套用

計算矩陣的秩的一個有用套用是計算線性方程組解的數目。如果係數矩陣的秩等於增廣矩陣的秩，則方程組只要有一個解。在這種情況下，它有精確的一個解，如果它的秩等於方程的數目。如果增廣矩陣的秩大於係數矩陣的秩，則通解有k個自由參量，這裡的k是在方程的數目和秩的差。否則方程組是不一致的。

在控制論中，矩陣的秩可以用來確定線性系統是否為可控制的，或可觀察的。