QR（正交三角）分解法是求一般矩陣全部特徵值的最有效並廣泛套用的方法，一般矩陣先經過正交相似變化成為Hessenberg矩陣，然後再套用QR方法求特徵值和特徵向量。它是將矩陣分解成一個正規正交矩陣Q與上三角形矩陣R，所以稱為QR分解法，與此正規正交矩陣的通用符號Q有關。
如果實（復）非奇異矩陣A能夠化成正交（酉）矩陣Q與實（復）非奇異上三角矩陣R的乘積，即A=QR，則稱其為A的QR分解。
基本介紹
- 中文名：QR分解
- 外文名：QR decomposition
- 別稱：正交三角分解法
分解方法,分解流程,實用意義,套用領域,
分解方法
這裡給出一個利用Householder變換的QR分解方法，給定mxn階實矩陣，m≥n，本算法計算Householder矩陣H1H2...Hn滿足：如果Q=H1H2...Hn，則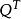
A=R是上三角矩陣，A1的上三角部分被R的上三角部分覆蓋，第j個Householder向量的j+1：m分量儲存於A（j+1：m，j），j<m.
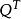
for j=1:n
[v,β]=house（A（j：m，j））
A（j：m，j：n）=（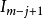
－βV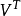
）A(j：m，j：n)
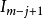
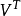
if j<m
A（j+1：m，j）=v（2：m－j+1）
end
end
在Matlab中，語法為[Q,R]=qr(A)或者[Q,R,perm] = qr(A,0)，如果A是一個m×n的矩陣，其QR分解後，Q為一個m×m的酉矩陣，R是一個m×n的上三角矩陣。
分解流程
（1）對需要求解的特徵值的矩陣進行QR分解
（2）對分解出來的結果進行逆向相乘
（3）將相乘得到的矩陣進行QR分解
（4）對分解出來的結果進行逆向相乘
實用意義
使用qr分解有助於加快解方程或求解速度即收斂速度。
套用領域
系統辨識是現代控制理論的重要組成部分。對系統的結構和參數進行辨識在工程上和理論上都占有重要的地位。最小二乘法是系統參數辨識中的重要估計方法,並在眾多領域和場合得到了廣泛的套用。
