若矩陣A=[a1,a2,…,an]∈Cm×n為復矩陣,則其列向量的所有線性組合的集合構成一個子空間,稱為矩陣A的列空間(column space)或列張成(column span),用符號CoI(A)表示。
基本介紹
- 中文名:列空間
- 外文名:column space
- 別名:列張成
- 所屬學科:數學(矩陣)
- 相關概念:復矩陣,列向量等
基本介紹
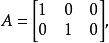

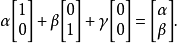
列空間與線性方程組










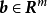


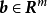







相關定理




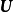
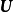
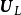
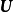
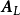
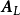
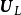

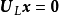
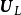
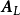
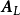



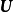
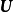

若矩陣A=[a1,a2,…,an]∈Cm×n為復矩陣,則其列向量的所有線性組合的集合構成一個子空間,稱為矩陣A的列空間(column space)或列張成(column span),用符號CoI(A)表示。
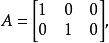

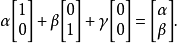










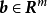


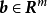











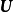
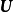
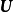
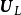
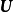
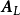
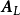
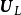

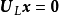
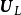
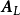
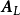



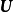
若矩陣A=[a1,a2,…,an]∈Cm×n為復矩陣,則其列向量的所有線性組合的集合構成一個子空間,稱為矩陣A的列空間(column space)或列張成(column span),用符號...
零空間是線上性映射(即矩陣)的背景下出現的,指:像為零的原像空間,即{x| Ax=0}。在數學中,一個運算元 A 的零空間是方程 Av = 0 的所有解 v 的集合。它...
空間陳列是指利用展示櫃、陳列架上方等通常情況下使用不到的地方陳列商品的陳列方法。適用此種陳列方法的商品主要有具有一定關聯性的商品,中小型且具有穩定感的商品,...
設V是數域P上的一個向量空間,若存在V的有限個向量α1,α2,...,αm使得V的每一個向量均為這m個向量的線性組合,則V稱為數域P上的一個有限維向量空間,...
零空間(北京)科技有限公司於2010-07-09成立。法定代表人朱海霞,公司經營範圍包括:技術開發、技術推廣、技術轉讓、技術諮詢、技術服務等。...
線上性代數中,零空間的維度又稱零度...... 線上性代數中,零空間的維度又稱零度V百科往期回顧 詞條統計 瀏覽次數:次 編輯次數:2次歷史版本 最近更新: 創建者:0...
《展陳空間設計》是2017年清華大學出版社出版的圖書,作者陳雷、劉斯暘、孫小茜、原泉、柳志宇、鄭琦凡。...
《世界經典設計50例:零售空間》是2001年1月1日上海文藝出版社出版的圖書,作者斯達福德·科里夫...
商業零售空間室內設計是室內設計中一項複雜的專業課程,具有設計對象的功能類型複雜、涉及內容廣泛、需解決問題眾多以及與施工聯繫密切等特點。這本由周昕濤、陳悅編著...
上海零空間汽車文化發展有限公司(簡稱“零空間汽車文化”或“零空間”),專業汽車場地一站式服務商。...
零點空間科技(北京)有限公司於2015-02-04在東城分局登記成立。法定代表人王順利,公司經營範圍包括銷售食品;技術推廣服務;機械設備租賃;項目投資等。...
秩是線性代數術語,線上性代數中,一個矩陣A的列秩是 A的線性無關的縱列的極大數目。類似地,行秩是 A的線性無關的橫行的極大數目。矩陣的列秩和行秩總是相等...
陳列是指把商品有規律地集中展示給顧客。商品陳列的目標是占據更多的陳列空間、儘可能地增加貨架上的陳列產品數量。陳列包括以下幾個原則:客流方向,陳列順序,陳列方向...
為充分利用向量空間,克服"假溢出"現象的方法是:將向量空間想像為一個首尾相接的圓環,並稱這種向量為循環向量。存儲在其中的佇列稱為循環佇列(Circular Queue)。...
“矩陣代數”課程,本書是在其講稿的基礎上,進行增刪、改寫而成的,書中詳細、準確地介紹了矩陣的列空間與核空間、矩陣對分解與標準形、向量範數、矩陣序列的極限...
《看圖學藝(服裝篇):圖解服飾陳列技巧》詳細論述了服飾陳列的概念,服飾陳列的規劃、位置和原則,服飾陳列的形式美法則與空間設計技巧,色彩搭配技巧與風格體現,設計...
《看圖學藝(服裝篇):圖解服飾陳列技巧》詳細論述了服飾陳列的概念,服飾陳列的規劃、位置和原則,服飾陳列的形式美法則與空間設計技巧,色彩搭配技巧與風格體現,設計...
