分塊矩陣是高等代數中的一個重要內容,是處理階數較高的矩陣時常採用的技巧,也是數學在多領域的研究工具。對矩陣進行適當分塊,可使高階矩陣的運算可以轉化為低階矩陣的運算,同時也使原矩陣的結構顯得簡單而清晰,從而能夠大大簡化運算步驟,或給矩陣的理論推導帶來方便。有不少數學問題利用分塊矩陣來處理或證明,將顯得簡潔、明快。
分塊矩陣是一個矩陣, 它是把矩陣分別按照橫豎分割成一些小的子矩陣 。 然後把每個小矩陣看成一個元素。
基本介紹
- 中文名:分塊矩陣
- 外文名:partitioned matrix
- 類別:矩陣
- 學科:高等數學
- 特殊:分塊對角矩陣,分塊上三角矩陣
- 相關:求解線性方程組
定義




運算規則
加法




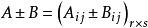
數乘



乘法






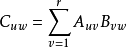

轉置




特殊分塊矩陣
分塊對角矩陣





分塊上下三角矩陣




