埃爾米特矩陣又稱自共軛矩陣、Hermite陣。Hermite陣中每一個第i 行第j 列的元素都與第j 行第i 列的元素的共軛相等(然而矩陣A的共軛矩陣並非Hermite陣)。自共軛矩陣是矩陣本身先轉置再把矩陣中每個元素取共軛得到的矩陣。
基本介紹
- 中文名:共軛矩陣
- 外文名:conjugate matrix
- 別稱:自共軛矩陣、Hermite陣
基本信息
 共軛矩陣表達式
共軛矩陣表達式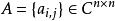


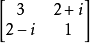
性質





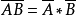
序列
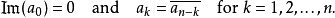
埃爾米特矩陣又稱自共軛矩陣、Hermite陣。Hermite陣中每一個第i 行第j 列的元素都與第j 行第i 列的元素的共軛相等(然而矩陣A的共軛矩陣並非Hermite陣)。自共軛矩陣是矩陣本身先轉置再把矩陣中每個元素取共軛得到的矩陣。
 共軛矩陣表達式
共軛矩陣表達式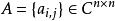


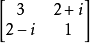





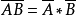
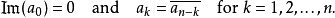
埃爾米特矩陣又稱自共軛矩陣、Hermite陣。Hermite陣中每一個第i 行第j 列的元素都與第j 行第i 列的元素的共軛相等(然而矩陣A的共軛矩陣並非Hermite陣)。自共軛...
若矩陣A、B維數相同,則(A + B)* = A* + B*。(rA)* = r*A*,其中r為複數,r*為r的復共軛。...
共軛在數學、物理、化學、地理等學科中都有出現。 本意:兩頭牛背上的架子稱為軛,軛使兩頭牛同步行走。共軛即為按一定的規律相配的一對。通俗點說就是孿生。在...
厄米特矩陣(Hermitian Matrix,又譯作“埃爾米特矩陣”或“厄米矩陣”),指的是自共軛矩陣。矩陣中每一個第i行第j列的元素都與第j行第i列的元素的共軛相等。...
埃爾米特矩陣(又稱“自共軛矩陣”)是共軛對稱的方陣。埃爾米特矩陣中每一個第i 行第j 列的元素都與第j 行第i 列的元素的共軛相等。n階複方陣A的對稱單元互...
共軛線性運算元(conjugate linear operator)是由線性運算元誘導出的共軛空間之間的運算元。...
在數學裡,作用於一個有限維的內積空間,自共軛矩陣。矩陣中每一個第i 行第j 列的元素都與第j 行第i 列的元素的共軛相等;等價地說,表達自伴運算元的矩陣是埃爾...
在數學中,矩陣(Matrix)是一個按照長方陣列排列的複數或實數集合,最早來自於方程組的係數及常數所構成的方陣。這一概念由19世紀英國數學家凱利首先提出。矩陣是高等...
矩陣範數(matrix norm)是數學中矩陣論、線性代數、泛函分析等領域中常見的基本概念,是將一定的矩陣空間建立為賦范向量空間時為矩陣裝備的範數。套用中常將有限維賦...
