光滑流是滿足某些條件的映射。微分流形M上任一有緊支集的光滑向量場在M上產生一個光滑流。
基本介紹
- 中文名:光滑流
- 外文名:smooth flow
- 適用範圍:數理科學
簡介
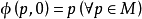

光滑流是滿足某些條件的映射。微分流形M上任一有緊支集的光滑向量場在M上產生一個光滑流。
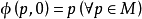

光滑流是滿足某些條件的映射。微分流形M上任一有緊支集的光滑向量場在M上產生一個光滑流。...
《光滑流形導論》是2008年3月1日世界圖書出版公司出版的圖書,作者是李(Lee,J.M)。本書主要介紹了光滑結構,切向量和余向量,向量叢,李導數,浸入和嵌入式子流形...
若對每個點p∈M,存在p的一個鄰域U,及存在U上的c個光滑向量場X1,X2,...,Xc,使這些光滑向量場在U中每點張成𝒟,則稱𝒟為光滑分布。...
數學中,里奇平坦流形(Ricci-flat manifold)是里奇張量為零的黎曼流形。在物理學中,它們代表了愛因斯坦方程在任何維數之黎曼流形且宇宙常數為零的類比,其所具有的...
極大積分流形(maximal integral manifold)是某種意義下為極大的積分流形。設(N,ψ)是流形M的分布D的連通積分流形,且其像不是D的其他連通積分流形的真子集,...
Ck流形(Ck manifold)是有Ck類微分結構的拓撲流形。Ck(k>1)流形統稱為微分流形。...... 當k=∞時,也稱M為光滑流形。Ck(k>1)流形統稱為微分流形。...
巴拿赫流形是有限維流形的無窮維推廣,巴拿赫流形一般均指巴拿赫微分流形,光滑流形一般是指C∞流形。...
積分流形(integral manifold)是一類子流形。它是由對合分布確定的子流形。流形是一類拓撲空間,它在每一點的附近都與歐氏空間同胚。一般的流形概念,起始於對於可...
氣液兩相流中,不同的流量、壓力、管路布置狀況和管道幾何形狀都會造成相界面的形狀(分布)的不同,即形成不同的流動結構模式,對此稱為流型(流態,流譜)。流型表示...
積流形(product manifold)是由兩個微分流形的笛卡兒積所生成的流形。...... 微分流形也稱為光滑流形,是拓撲學和幾何學中一類重要的空間,是帶有微分結構的拓撲流...
代數流形(algebraic manifold)是復射影空間中的代數子集。若P(C)的一個子流形是P(C)的一個代數子集,則稱這個復子流形為代數子流形。若一個復流形是雙全...
在數學中,拉格朗日-格拉斯曼流形是一種典型的格拉斯曼流形,有著重要的研究地位。...... 流形(Lagrangian-Grassmannian)是實辛向量空間中拉格朗日子空間上的光滑流形...
4維可微流形唐納森定理(Donaldson theo-rem on differentiable 4-manifolds)關於可微4維流形相交性質的一個定理.考察可微流形的情形,於此一個重要的事實是,與拓撲...
n維流形,拓撲空間<math>\mathcal</math>在滿足以下條件時,稱<math>\mathcal</math>為<math>m</math>維流形,即 <math>\mathcal</math>為豪斯多夫空間,...
若在光滑流形M上指定了一個聯絡 ,則稱(M, )為仿射聯絡空間。設(M, )是一個仿射聯絡空間,在局部坐標系(U;x)下,若:則稱Γkij為聯絡在該坐標系下的係數...
球面定理是3維流形理論中的一個基本定理。若M為3維可定向流形,π2(M)≠0,則在M中存在一個PL球面S²,使得S²在M中不同倫於0。對於不可定向流形,相當...
數學上,霍奇理論是光滑流形M的代數拓撲的研究的一個方面。...... 數學上,霍奇理論是光滑流形M的代數拓撲的研究的一個方面。更精確的講,它尋找M的實係數上同調...
n維歐氏空間是n維流形的典型例子,事實上也就是光滑流形。對於 ,任意與 同胚的可微n維流形,也是微分同胚的。值得驚奇的結果是,1982年西蒙·唐納森證明了對於 的...
