信息量

信息量是指信息多少的量度。1928年R.V.L.哈特萊首先提出信息定量化的初步構想，他將訊息數的對數定義為信息量。若信源有m種訊息，且每個訊息是以相等可能產生的，則該信源的信息量可表示為I=logm。但對信息量作深入而系統研究，還是從1948年C.E.仙農的奠基性工作開始的。在資訊理論中，認為信源輸出的訊息是隨機的。即在未收到訊息之前，是不能肯定信源到底傳送什麼樣的訊息。而通信的目的也就是要使接收者在接收到訊息後，儘可能多的解除接收者對信源所存在的疑義（不定度），因此這個被解除的不定度實際上就是在通信中所要傳送的信息量。

基本介紹

• 中文名：信息量
• 外文名：amount of information
• 套用學科：通信
• 領域：工程技術

歷史

1928年，R．V．L．哈特萊提出了信息定量化的初步構想，他將符號取值數m的對數定義為信息量，即I=log₂m。對信息量作深入、系統研究的是資訊理論創始人C．E．仙農。1948年，仙農指出信源給出的符號是隨機的，信源的信息量應是機率的函式，以信源的信息熵表示，即 ，其中P_i表示信源不同種類符號的機率，i= 1，2，…，n。

例如，若一個連續信源被等機率量化為4層，即4 種符號。這個信源每個符號所給出的信息最應為 ，與哈特萊公式I=log₂m=log₂4=2bit一致。實質上哈特萊公式是等機率時仙農公式的特例。

基本內容 實際信源多為有記憶序列信源，只有在掌握全部序列的機率特性後，才能計算出該信源中平均一個符號的熵H_L（U）（L為符號數這通常是困難的。如果序列信源簡化為簡單的一階、齊次、遍歷馬氏鏈，則比較簡單。根據符號的條件機率P_ji（即前一符號為i條件下後一符號為j的機率），可以求出遍歷信源的穩定機率P_i，再由P_i和P_ji求出H_L（U）。即如圖1 。

圖1

其中H（U|V）稱為條件熵，即前一符號V已知時後一符號U的不確定度。

信息量與信息熵在概念上是有區別的。在收到符號之前是不能肯定信源到底傳送什麼符號，通信的目的就是使接收者在收到符號後，解除對信源存在的疑義（不確定度），使不確定度變為零。這說明接收者從傳送者的信源中獲得的信息量是一個相對的量（H（U）-0）。而信息熵是描述信源本身統計特性的物理量，它表示信源產生符號的平均不確定度，不管有無接收者，它總是客觀存在的量。

從信源中一個符號V中獲取另一符號u的信息

量可用互信息表示，即

I（U；V）= H（U）-H（U|V）

表示在收到V以後仍然存在對信源符號U的疑義（不確定度）。一般情況下

I（U；V）≤H（U）

即獲得的信息量比信源給出的信息熵要小。

連續信源可有無限個取值，輸出信息量是無限大，但互信息是兩個熵值之差，是相對量。這樣，不論連續或離散信源，接收者獲取的信息量仍然保持信息的一切特性，且是有限值。

信息量的引入，使通信、信息以及相關學科得以建立在定量分析的基礎上，為各有關理論的確立與發展提供了保證。

簡介

所謂信息量是指從N個相等可能事件中選出一個事件所需要的信息度量或含量，也就是在辯識N個事件中特定的一個事件的過程中所需要提問"是或否"的最少次數.

香農（C. E. Shannon）資訊理論套用機率來描述不確定性。信息是用不確定性的量度定義的.一個訊息的可能性愈小，其信息愈多；而訊息的可能性愈大，則其信息愈少.事件出現的機率小，不確定性越多，信息量就大，反之則少。

信息現代定義。[2006年，醫學信息（雜誌），鄧宇等].

信息是物質、能量、信息及其屬性的標示。逆維納信息定義

信息是確定性的增加。逆香農信息定義

信息是事物現象及其屬性標識的集合。2002年

在數學上，所傳輸的訊息是其出現機率的單調下降函式。如從64個數中選定某一個數，提問：“是否大於32?”，則不論回答是與否，都消去了半數的可能事件，如此下去，只要問6次這類問題，就可以從64個數中選定一個數。我們可以用二進制的6個位來記錄這一過程，就可以得到這條信息。

信息多少的量度。1928年R.V.L.哈特萊首先提出信息定量化的初步構想，他將訊息數的對數定義為信息量。若信源有m種訊息，且每個訊息是以相等可能產生的，則該信源的信息量可表示為I=logm。但對信息量作深入而系統研究，還是從1948年C.E.香農的奠基性工作開始的。

信息的統計特徵描述是早在1948年香農把熱力學中熵的概念與熵增原理引入信息理論的結果。先行考察熵增原理。熱力學中的熵增原理是這樣表述的：存在一個態函式－熵，只有不可逆過程才能使孤立系統的熵增加，而可逆過程不會改變孤立系統的熵。從中可以看出：一、熵及熵增是系統行為；二、這個系統是孤立系統；三、熵是統計性狀態量，熵增是統計性過程量。討論信息的熵表述時，應充分注意這些特徵的存在。並且知道，給定系統中發生的信息傳播，是不可逆過程。

在資訊理論中，認為信源輸出的訊息是隨機的。即在未收到訊息之前，是不能肯定信源到底傳送什麼樣的訊息。而通信的目的也就是要使接收者在接收到訊息後，儘可能多的解除接收者對信源所存在的疑義（不定度），因此這個被解除的不定度實際上就是在通信中所要傳送的信息量。因此，接收的信息量在無干擾時，在數值上就等於信源的信息熵，式中P(xi）為信源取第i個符號的機率。但在概念上，信息熵與信息量是有區別的。信息熵是描述信源本身統計特性的一個物理量。它是信源平均不定度，是信源統計特性的一個客觀表征量。不管是否有接收者它總是客觀存在的。信息量則往往是針對接收者而言的，所謂接收者獲得了信息，是指接收者收到訊息後解除了對信源的平均不定度，它具有相對性。對於信息量的說明須引入互信息的概念。

E.H.Weber

在資訊理論中，互信息的定義是：I(X；Y)=H(X）－H(X|Y），數式右邊後一項稱為條件熵，對離散訊息可表示，它表示已知Y以後，對X仍存在的不定度。因此，互信息I(X;Y）是表示當收到Y以後所獲得關於信源X的信息量。與互信息相對應，常稱H(X)為自信息。互信息具有三個基本性質。

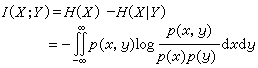公式

①非負性：I(X;Y）≥0，僅當收到的訊息與傳送的訊息統計獨立時，互信息才為0。

②互信息不大於信源的熵：I(X;Y）≤H(X），即接收者從信源中所獲得的信息必不大於信源本身的熵。僅當信道無噪聲時，兩者才相等。

公式

③對稱性：I(X;Y)=I(Y;X），即Y隱含X和X隱含Y 的互信息是相等的。

對於連續信源的互信息，它仍表示兩個熵的差值，所以也可直接從離散情況加以推廣，並保持上述離散情況的一切特性，即 實際信源是單個訊息信源的組合，所以實際信源的互信息I(X;Y）也可以直接從上述單個訊息的互信息I(X；Y）加以推廣，即I(X;Y)=H(X)-H(X│Y）。配圖相關連線

計算方法

資訊理論創始人C.E.Shannon，1938年首次使用比特（bit）概念：1（bit）= 。它相當於對二個可能結局所作的一次選擇量。資訊理論採用對隨機分布機率取對數的辦法，解決了不定度的度量問題。

m個對象集合中的第i個對象，按n個觀控指標測度的狀態集合的

全信息量TI= 。

從試驗後的結局得知試驗前的不定度的減少，就是申農界定的信息量，即

自由信息量FI=－∑pi ，（i=1,2，…，n）。

式中pi是與隨機變數xi對應的觀控權重，它趨近映射其實際狀態的分布機率。由其內在分布構成引起的在試驗前的不定度的減少，稱為先驗信息或謂約束信息量。風險是潛藏在隨機變數尚未變之前的內在結構能（即形成該種結構的諸多作用中還在繼續起作用的有效能量）中的。可以顯示、映射這種作用的是

約束信息量BI=TI-FI。

研究表明，m個觀控對象、按n個觀控指標進行規範化控制的比較收益優選序，與其自由信息量FI之優選序趨近一致；而且各觀控對象“愈自由，風險愈小”；約束信息量BI就是映射其風險的本徵性測度，即風險熵。

把信息描述為信息熵，是狀態量，其存在是絕對的；信息量是熵增，是過程量，是與信息傳播行為有關的量，其存在是相對的。在考慮到系統性、統計性的基礎上，認為：信息量是因具體信源和具體信宿範圍決定的，描述信息潛在可能流動價值的統計量。本說法符合熵增原理所要求的條件：

一、“具體信源和信宿範圍”構成孤立系統，信息量是系統行為而不僅僅是信源或信宿的單獨行為。

二、界定了信息量是統計量。此種表述還說明，信息量並不依賴具體的傳播行為而存在，是對“具體信源和具體信宿”的某信息潛在可能流動價值的評價，而不是針對已經實現了的信息流動的。由此，信息量實現了信息的度量。

計算過程

如何計算信息量的多少？在日常生活中，極少發生的事件一旦發生是容易引起人們關注的，而司空見慣的事不會引起注意，也就是說，極少見的事件所帶來的信息量多。如果用統計學的術語來描述，就是出現機率小的事件信息量多。因此，事件出現得機率越小，信息量愈大。即信息量的多少是與事件發生頻繁（即機率大小）成反比。

⒈如已知事件Xi已發生，則表示Xi所含有或所提供的信息量

H(Xi) = −

例題：若估計在一次西洋棋比賽中謝軍獲得冠軍的可能性為0.1（記為事件A），而在另一次西洋棋比賽中她得到冠軍的可能性為0.9（記為事件B）。試分別計算當你得知她獲得冠軍時，從這兩個事件中獲得的信息量各為多少？

H(A)=- ≈3.32（比特）

H(B)=- ≈0.152（比特）

⒉統計信息量的計算公式為：

Xi —— 表示第i個狀態（總共有n種狀態）；

P(Xi）——表示第i個狀態出現的機率；

H(X）——表示用以消除這個事物的不確定性所需要的信息量。

例題：向空中投擲硬幣，落地後有兩種可能的狀態，一個是正面朝上，另一個是反面朝上，每個狀態出現的機率為1/2。如投擲均勻的正六面體的骰子，則可能會出現的狀態有6個，每一個狀態出現的機率均為1/6。試通過計算來比較狀態的不肯定性與硬幣狀態的不肯定性的大小。

H（硬幣）= -（2×1/2）× ≈1（比特）

H（骰子）= -（1/6×6）× ≈2.6（比特）

由以上計算可以得出兩個推論：

[推論1] 若且唯若某個P(Xi)=1，其餘的都等於0時， H(X)= 0。

[推論2]若且唯若某個P(Xi)=1/n，i=1， 2，……， n時，H(X）有極大值log n。

發展過程

如今被稱為信息化社會，現代情報學理論及其套用，非常注重信息量化測度。1980年代，英國著名情報學家B.C.布魯克斯，在闡述人之信息（情報）獲取過程時，深入研究了感覺信息的接收過程，並將透視原理──對象的觀察長度Z與從觀察者到被觀察對象之間的物理距離X成反比，引入情報學，提出了Z= 的對數假說。用此能較好地說明信息傳遞中，情報隨時間、空間、學科（行業）的不同而呈現的對數變換。然而，關於用戶的情報搜尋行為，在其信息來源上，“獲取距離最近的比例最高，最遠的比例最低”的結論，在跨域一體、存在國際網際網路，需要有新的理論進行新的概括。對數透視變換，源於實驗心理物理學。1846年德國心理學家E.H.Weber提出了韋伯公式：△I/I=k。這裡，△I代表剛可感覺到的差別閾限，I代表標準刺激物理量，k是小於1的常數。後來，Fechner把這個關於差別閾限的規律稱之為韋伯定律，並於1860年在此基礎上提出了著名的費肯納對數定律：心理的感覺量值S是物理刺激量I的對數函式，即S=cLogI，c是由特殊感覺方式確定的常數。

1957年Stevens提出冪定律：S=bIa，a與b為特徵常數。心理物理函式究竟是服從冪定律還是服從對數定律？W.S.Togerson認為，這不能通過實驗解決，而是一個在實驗中進行選擇的問題。G.Ekman在假定Fechner的對數定律是普遍正確的前提下，推導出冪定律是對數定律的一個特例。

中國有突出貢獻的科學家程世權，在1990年出版的《模糊決策分析》一書中，評介引述於宏義等對“系統的定性和定量轉化，總結歸納出了一種方便可行、科學可靠的定性排序與定量轉化的方法”。於宏義等之方法，在利用顯在的頻數信息的同時，巧妙利用了潛在的泛序信息——權數，使模糊系統簡便有效地轉化成明晰的工程系統。其測度模式是：

F(I)=Ln(max{I}-I+2）/Ln(max{I}+1）。

式中，I為所論對象按一定指標的排序序號，F(I）為其隸屬度。實際套用中巧妙運用“自動連鎖”機制，確實簡便、實用、有效。所謂“自動連鎖”機制，就是“評價者在評價他人他事他物的同時，不能不表現自身，不能不被評價”。