基本介紹
- 中文名:正六面體
- 外文名:cube
- 別稱:立方體、正方體
- 學科:數學
- 屬性:屬於六面體、是特殊的長方體
- 特徵:6個面形狀相同,每條棱長度相等
特徵
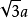
表面積和體積
表面積
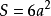
體積

相關概念
體對角線
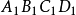
 圖1
圖1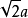
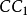
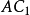
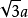
單位體積
球半徑
平面截正方體
展開圖




優美定值
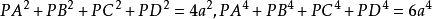
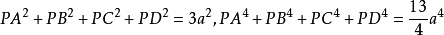
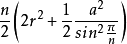


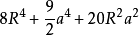
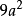
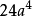
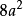
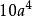

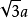
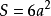

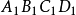
 圖1
圖1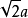
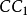
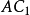
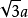




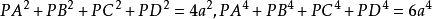
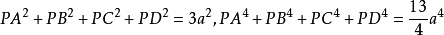
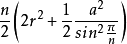


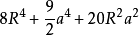
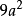
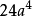
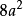
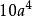
用六個完全相同的正方形圍成的立體圖形叫正六面體,也稱立方體、正方體。正六面體是一種側面和底面均為正方形的直平行六面體,即棱長都相等的六面體。正六面體是特殊...
六面體就是有六個面的空間形體,共分為正六面體(也叫正方體)、平行六面體、不規則六面體三類。棱長相等的長方體叫做正方體,又稱“立方體”、“正六面體”。底面...
其中面數最少的是正四面體,面數最多的是正二十面體。有些化學物質的結晶體呈正多面體的形狀,如食鹽的結晶體是正六面體,明礬的結晶體是正八面體。...
五複合正六面體(英語:Compoundoffivecubes,又稱為Cube5-Compound),是一種凹多面體,屬於星形多面體,外觀看起來像很多正六面體卡在一起。這可以被看作是多面體和星形...
正多面體的種數很少。多面體可以有無數,但正多面體只有正四面體、正六面體、正八面體、正十二面體、正二十面體五種。其中面數最少的是正四面體,面數最多的是...
正四面體 正六面體 正八面體 正十二面體 正二十面體 五種正多面體 面的種類 頂點個數 棱個數 圍繞一個頂點的面的個數 面個數 正四面體 正三角形 ...
由歐拉定理推出:凸正多面體只有五種,即:正四面體、正八面體、正二十面體、正六面體(正方體)、正十二面體,其中正四面體、正八面體和正二十面體的各面都是正...
三複合正六面體(英語:Compoundofthreecubes,又稱為Cube3-Compound),是一種凹多面體,屬於星形多面體,外觀看起來像三個正六面體卡在一起。這可以被看作是多面體和...
解釋:甲烷為正四面體結構,若將四種化學集團視為四種不同“顏色”,該問題等價於正四面體的頂點進行四染色問題。例4:在正六面體的每個面上任意做一條對角線,有多少...
立方體,也稱正方體,是由6個正方形面組成的正多面體,故又稱正六面體。它有12條邊和8個頂點。其中正方體是特殊的長方體。
柏拉圖立體,是都只由一種正多邊形構成各面的體,被稱為最有規律的立體結構。...▪ 正六面體 ▪ 正八面體 ▪ 正十二面體 ▪ 正二十面體 柏拉圖...
在60度視域中,觀察正六面體上下、前後、兩側三個面,不論立方體在什麼位置,只要有一個面與可視畫面平行,立方體和畫面所構成的透視關係透視就叫“平行透視”。(它只有...
用六個完全相同的正方形圍成的立體圖形叫正方體。側面和底面均為正方形的直平行六面體叫正方體,即棱長都相等的六面體,又稱“立方體”“正六面體”。正方體是特殊...
在正六面體上下、前後、兩側三個面中,只要有一個面與畫面平行,同時有一面與地面平行的正方面體透視就叫“平行透視”。(它只有一個消失點)正六面體的平行透視最少...
