理論提出 資訊理論 之父 C. E. Shannon 在 1948 年發表的論文“通信的數學理論( A Mathematical Theory of Communication )”中指出,任何信息都存在冗餘,冗餘大小與信息中每個符號(數字、字母或單詞)的出現機率或者說不確定性有關。
Shannon 借鑑了熱力學的概念,把信息中排除了冗餘後的平均信息量稱為“信息熵”,並給出了計算信息熵的數學表達式。
基本內容 通常,一個信源傳送出什麼符號是不確定的,衡量它可以根據其出現的機率來度量。機率大,出現機會多,不確定性小;反之不確定性就大。
不確定性函式f是機率P的
減函式 ;兩個獨立符號所產生的不確定性應等於各自不確定性之和,即f(P
1, P
2 )=f(P
1 )+f(P
2 ),這稱為可加性。同時滿足這兩個條件的函式f是對數函式,即
。
在信源中,考慮的不是某一單個符號發生的不確定性,而是要考慮這個信源所有可能發生情況的平均不確定性。若信源符號有n種取值:U
1 …U
i …U
n ,對應機率為:P
1 …P
i …P
n ,且各種符號的出現彼此獨立。這時,信源的平均不確定性應當為單個符號不確定性-logP
i 的統計平均值(E),可稱為信息熵,即
,式中對數一般取2為底,單位為比特。但是,也可以取其它對數底,採用其它相應的單位,它們間可用換底公式換算。
最簡單的單符號信源僅取0和1兩個元素,即二元信源,其機率為P和Q=1-P,該信源的熵即為如圖1所示。
由圖可見,離散信源的信息熵具有:
①非負性:即收到一個信源符號所獲得的信息量應為正值,H(U)≥0
②對稱性:即對稱於P=0.5
③確定性:H(1,0)=0,即P=0或P=1已是確定狀態,所得信息量為零
④極值性:因H(U)是P的上凸函式,且一階導數在P=0.5時等於0,所以當P=0.5時,H(U)最大。
對連續信源,香農給出了形式上類似於離散信源的連續熵,雖然連續熵
仍具有可加性,但不具有信息的非負性,已不同於離散信源。
不代表連續信源的信息量。連續信源取值無限,信息量是無限大,而
是一個有限的相對值,又稱相對熵。但是,在取兩熵的差值為互信息時,它仍具有非負性。這與力學中勢能的定義相仿。
圖1 二元信源的熵 信息含義 現代定義 信息是
物質、能量 、信息及其屬性的標示 。【
逆維納 信息定義】
信息是確定性的增加 。【逆香農 信息定義】
信息是事物現象及其屬性標識 的集合。【2002年】
最初定義 信息理論的鼻祖之一Claude E. Shannon把信息(熵)定義為
離散 隨機事件 的出現機率。
所謂信息熵,是一個
數學 上頗為抽象的概念,在這裡不妨把信息熵理解成某種特定信息的出現機率。而信息熵和熱力學熵是緊密相關的。根據Charles H. Bennett對Maxwell's Demon的重新解釋,對信息的銷毀是一個不可逆過程,所以銷毀信息是符合
熱力學第二定律 的。而產生信息,則是為系統引入負(
熱力學 )熵的過程。所以信息熵的符號與熱力學熵應該是相反的。
一般而言,當一種信息出現機率更高的時候,表明它被傳播得更廣泛,或者說,被引用的程度更高。我們可以認為,從信息傳播的角度來看,信息熵可以表示信息的價值。這樣子我們就有一個衡量信息價值高低的標準,可以做出關於知識流通問題的更多推論。
計算公式 H(x) = E[I(xi )] = E[ log(2,1/P(xi )) ] = -∑P(xi )log(2,P(xi )) (i=1,2,..n)
其中,x表示隨機變數,與之相對應的是所有可能輸出的集合,定義為符號集,隨機變數的輸出用x表示。P(x)表示輸出機率函式。變數的不確定性越大,熵也就越大,把它搞清楚所需要的信息量也就越大.
《博弈聖經》 信息熵:信息的基本作用就是消除人們對事物的不確定性。多數粒子組合之後,在它似像非像的形態上押上有價值的數碼,具體地說,這就是一個在博弈對局中信息混亂的現象。
-(p1*log(2,p1) + p2 * log(2,p2) + ... +p32 *log(2,p32)),
其中,p1,p2 , ...,p32 分別是這 32 個球隊奪冠的機率。香農把它稱為“信息熵” (Entropy),一般用符號 H 表示,單位是比特。
信息熵 有興趣的讀者可以推算一下當 32 個球隊奪冠機率相同時,對應的信息熵等於五比特。有數學基礎的讀者還可以證明上面公式的值不可能
大於五 。對於任意一個隨機變數 X(比如得冠軍的球隊),它的熵定義如下:
變數的不確定性越大,熵也就越大,把它搞清楚所需要的信息量也就越大。
信息熵是
資訊理論 中用於度量信息量的一個概念。一個系統越是有序,信息熵就越低;
反之,一個系統越是混亂,信息熵就越高。所以,信息熵也可以說是系統
有序化 程度的一個度量。
假定有兩種氣體a、b,當兩種氣體完全混合時,可以達到熱物理學中的穩定狀態,此時熵最高。如果要實現反向過程,即將a、b完全分離,在封閉的系統中是沒有可能的。只有外部干預(信息),也即系統外部加入某種
有序化 的東西(
能量 ),使得a、b分離。這時,系統進入另一種穩定狀態,此時,信息熵最低。熱物理學證明,在一個封閉的系統中,熵總是增大,直至最大。若要使系統的熵減少(使系統更加
有序化 ),則必須有外部
能量 的干預。
信息熵的計算是非常複雜的。而具有多重前置條件的信息,更是幾乎不能計算的。所以在現實世界中信息的價值大多是不能被計算出來的。但因為信息熵和熱力學熵的緊密相關性,所以信息熵是可以在衰減的過程中被測定出來的。因此信息的價值是通過信息的傳遞體現出來的。在沒有引入附加價值(
負熵 )的情況下,傳播得越廣、流傳時間越長的信息越有價值。
熵首先是物理學裡的名詞。
在傳播中是指信息的不確定性,一則高信息度的信息熵是很低的,低信息度的熵則高。具體說來,凡是導致
隨機事件 集合的肯定性,組織性,法則性或有序性等增加或減少的活動過程,都可以用信息熵的改變數這個統一的標尺來度量。
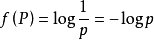
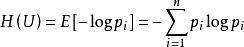
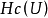
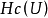
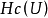
 圖1 二元信源的熵
圖1 二元信源的熵 信息熵
信息熵