基本介紹
- 中文名:企鵝圖
- 外文名:Penguin diagram
- 領域:量子力學
歷史
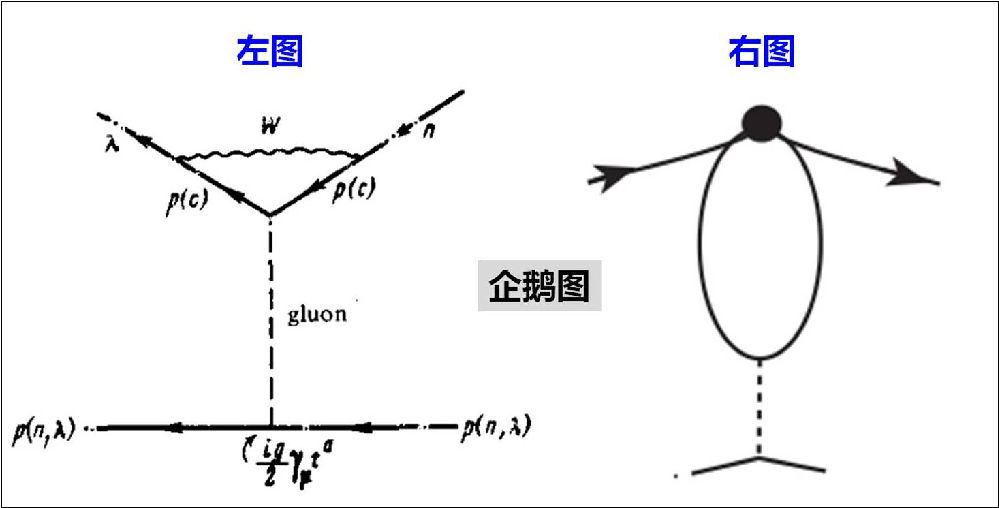
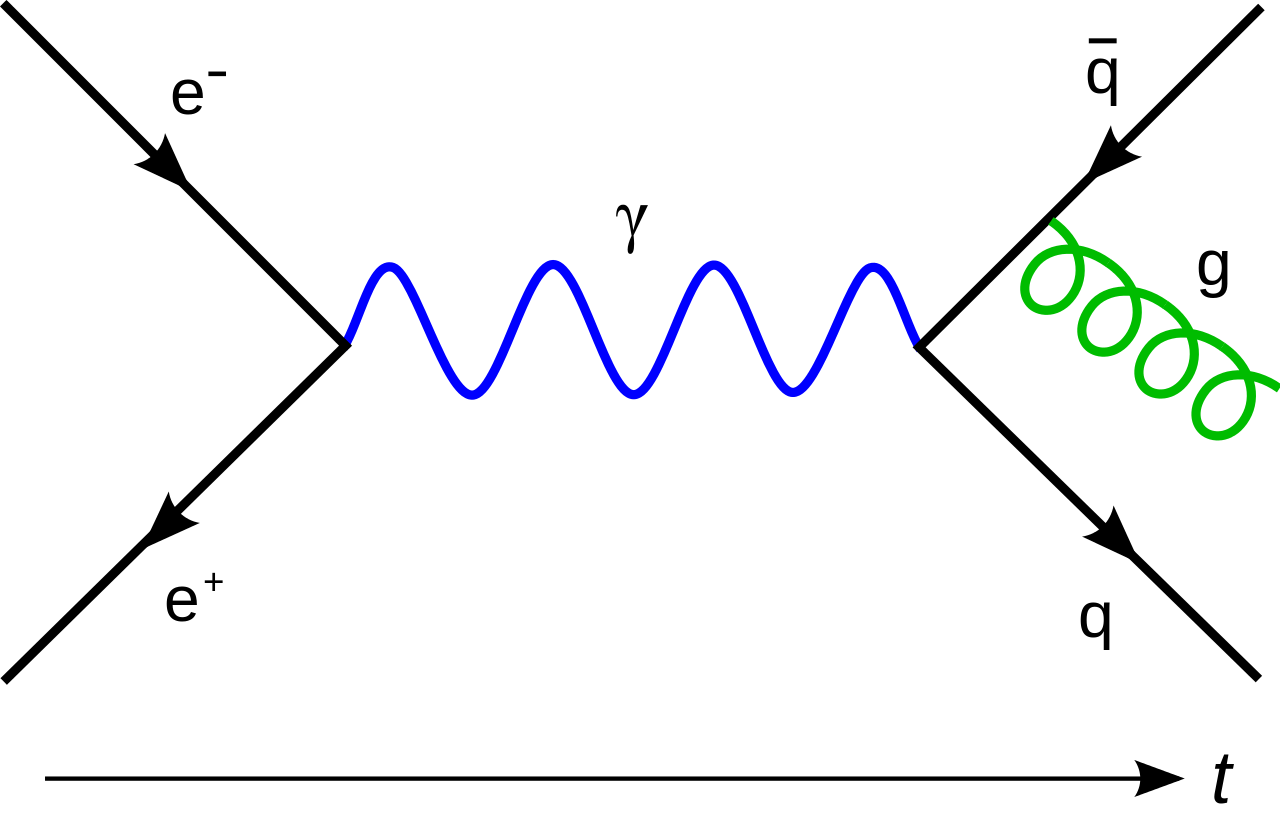
費曼圖
動機與歷史
其他名稱
味

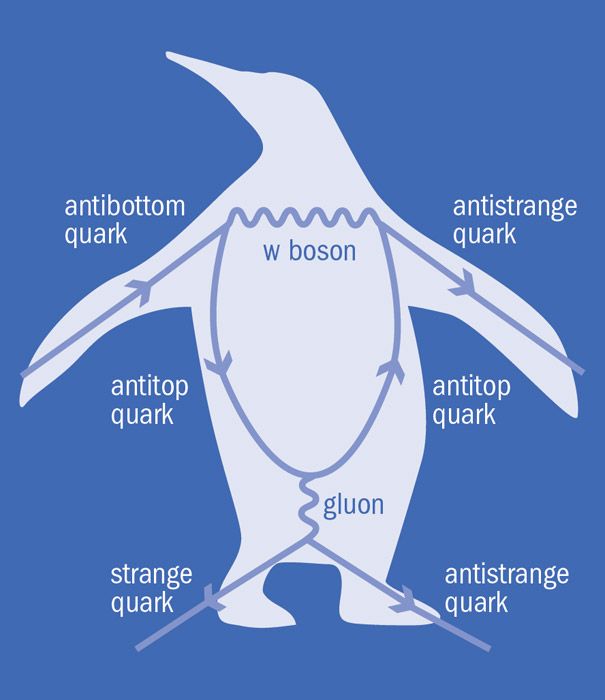



在量子場論中,企鵝圖是一類費曼圖,對於理解標準模型中的CP破壞過程很重要。它們是指夸克暫時改變味的單循環過程(通過W或Z循環),味道變化的夸克參與某種樹相互作用,通常是強相互作用。對於某些夸克味,相互作用幅度比其他夸克味更大的相互作用,如CP破壞或Higgs相互作用,這些企鵝進程的幅度可能與直接樹進程的幅度...
帝企鵝是企鵝目企鵝科王企鵝屬鳥類。帝企鵝一般身高在90—120厘米,體重達50千克。其形態特徵是脖子底下有一片橙黃色羽毛,向下逐漸變淡,耳朵後部最深;全身色澤協調,頸部為淡黃色;耳朵的羽毛為鮮黃橘色,腹部乳白色;背部及鰭狀肢則是黑色,鳥喙的下方是鮮橘色。帝企鵝壽命一般在10年左右。帝企鵝分布在南極大陸...
王企鵝是企鵝目企鵝科王企鵝屬的鳥類,又名國王企鵝。身高95厘米左右;嘴巴細長;胸骨具有發達的龍骨突起;前肢發育成鰭;腳上帶有蹼;羽毛呈鱗片狀,排列緻密;尾巴上的羽毛較短。頭、喙、脖子等部位呈橘色。外形與帝企鵝相似,但身材比帝企鵝略苗條。王企鵝分布在極地冷水和北部溫水交匯的南極幅合帶。棲息地遍布...
小藍企鵝是企鵝目企鵝科小藍企鵝屬動物。小藍企鵝頭部和背部的羽毛呈靛藍色,耳部呈青灰色,腹部的羽毛則為白色,前肢外部為靛藍色,內側呈白色;喙是深灰黑色,長約3至4厘米,腳部朝上的一面為白色,腳底和蹼則是黑色。未成年的小藍企鵝的喙顯得比較短,頭部和背部羽毛的顏色也比較淺。雄性小藍企鵝的體型比雌性的...
斑嘴環企鵝是企鵝目企鵝科環企鵝屬鳥類。體長63厘米。體呈板石色;頭的背和上面有一半圓形白色花紋向下延伸;一條馬蹄形狹窄黑線沿體側後伸並橫跨胸部,延伸到兩邊的肋部;眼周圍和上方有肉紅色斑。兩翼演變退化成鰭狀,通體羽毛細小呈鱗狀;生有三個腳趾,趾間生蹼,還有一小趾分生在後方。斑嘴環企鵝主要分布...
洪堡企鵝,是企鵝目企鵝科 環企鵝屬 鳥類動物。洪堡企鵝身高約74厘米,胸前有單條黑色羽毛帶,下頦基部有一條肉粉色條紋延伸至眼睛;面部是裸露的,顯露出肉粉色的皮膚;額頭比其他所有企鵝都更為突出,在腹部黑色環帶的邊緣,大多都有相對較多的小黑斑。因發現它的德國科學家是洪保而得名。洪堡企鵝分布在南北州西...
麥哲倫企鵝,是企鵝目企鵝科 環企鵝屬 企鵝 ,又叫麥氏環企鵝。身高約為60 厘米,體重4-6千克;嘴巴扁長,背部為黑色或褐色;腹部為白色,頭上有一個白環;名字來源於著名的航海家麥哲倫,因為是麥哲倫第一次環南美洲大陸航行時發現了這種企鵝。麥哲倫企鵝主要分布於南美洲阿根廷、智利和福克蘭群島沿海,有時在巴西...
(概述圖參考來源:)動物學史 馬可羅尼企鵝1837年由德國自然科學家約翰·弗里德里希·馮·勃蘭特(Johann Friedrich von Brandt)命名,它的學名“chrysolophus”取自古希臘語,為“金色頭冠”之意,這是因為馬可羅尼企鵝頭頂上有一束標誌性的金色羽毛。而“馬可羅尼”音譯自於英文通用名“Macaroni”,這種英文叫法...
帽帶企鵝,是企鵝目 企鵝科 阿德利企鵝屬 極地鳥類。體長約為43~53厘米,體重4千克,軀體呈流線型;背部的羽毛呈黑色,腹部的羽毛呈白色;翅膀已經退化成鰭形,羽毛則為呈披針型排列的細管狀結構;腳瘦腿短,趾間有蹼,尾巴十分短小;整個軀體顯得又肥又胖,行走蹣跚;脖子底下有一道像海軍軍官的帽帶一樣的黑色...
阿德利企鵝是企鵝目企鵝科阿德利企鵝屬鳥類。呈紡錘形。羽毛由黑、白兩色組成;頭部、背部、尾部、翼背面、下頜為黑色,其餘部分均為白色;眼周為白色;嘴為黑色,嘴角有細長羽毛;腿短,足為鉻黃色。因南極大陸的阿德利地而得名。壽命約20年。 阿德利企鵝主要分布在南極大陸、南極半島以及南設得蘭群島、南喬治亞島等...
南跳岩企鵝,又稱“鳳頭黃眉企鵝”,是鳥綱企鵝目企鵝科共有17種鳥類動物。其體長52-55厘米,體重為2.5-3千克。南跳岩企鵝體型小巧,長著紅色的眼睛、紅棕色的喙、兩道黃色的長眉毛,讓人印象深刻。它的家位於南冰洋的島嶼上,他們總是在石塊間跳來跳去,因此而得名。南跳岩企鵝分布在智利、阿根廷、福蘭克...
加島環企鵝是企鵝目企鵝科環企鵝屬鳥類,又稱加拉帕戈斯企鵝。背部呈黑色,腹部呈白色,並有一些黑色羽毛形成的斑點;一條白條從粉紅色的眼睛處延伸到另外一側,一條並不明顯的灰黑色的條紋穿過胸部;細長的鰭腳底部有淡淡的黃色;鰭腳下的羽毛從白色的下巴處延伸下來;鰭腳下裸露的皮膚和眼睛周圍的皮膚是粉紅色的,還...
(概述圖參考來源:)形態特徵 翹眉企鵝身高60-65厘米,體重約4-6.5千克。雄性體型一般都比較大。它們兩側眉毛上方各有一簇尖長的,像刷子一樣的黃色冠毛,這種柔軟光潔的羽毛使翹眉企鵝在相似的種類中顯得很突出。成鳥的頭部、喉嚨上部和臉頰的顏色是非常深的黑色。身體和上半部,連同尾巴,是藍黑色的,而下半...
白鰭企鵝是神仙企鵝的突變種,但也有人認為他們和神仙企鵝是同一種企鵝。他們不同的地方是白鰭企鵝的翅膀上有一層白圈,且較高較重,其餘的都和神仙企鵝一樣。(概述圖參考來源:)簡介 白鰭企鵝是神仙企鵝的突變種,但也有人認為他們和神仙企鵝是同一種企鵝。他們不同的地方是白鰭企鵝的翅膀上有一層白圈,...
