以機率1收斂(converges with probability one)亦稱幾乎必然收斂.、幾乎處處收斂、幾乎肯定收斂,是隨機變數列的一種較強的收斂性。若隨機變數列以機率1收斂,則它必然依機率收斂,反之則未必。
基本介紹
- 中文名:以機率1收斂
- 外文名:converges with probability one
- 別名:幾乎必然收斂、幾乎處處收斂等
- 所屬領域:機率論
- 相關概念:隨機變數列、依機率收斂等
定義













以機率1收斂的判別準則
定理











定理證明













推論




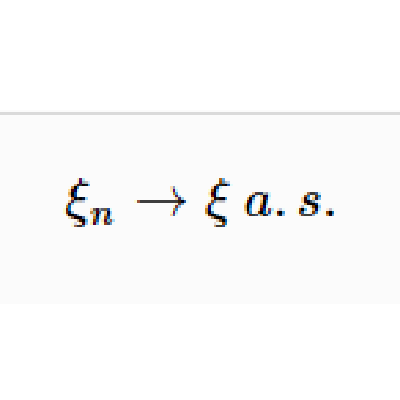
以機率1收斂(converges with probability one)亦稱幾乎必然收斂.、幾乎處處收斂、幾乎肯定收斂,是隨機變數列的一種較強的收斂性。若隨機變數列以機率1收斂,則它必然依機率收斂,反之則未必。









































以機率1收斂(converges with probability one)亦稱幾乎必然收斂.、幾乎處處收斂、幾乎肯定收斂,是隨機變數列的一種較強的收斂性。若隨機變數列以機率1收斂,則它必然依機率收斂,反之則未必。定義我...
強大數律(見大數律)就是闡明事件發生的頻率和樣本觀測值的算術平均分別以機率 1收斂於該事件的機率和總體的均值。以機率 1收斂也常稱為幾乎必然(簡記為.)收斂,它相當於測度論中的幾乎處處(簡記為..)收斂。若對任一正數ε,都...
依機率收斂,convergence in probability,別稱隨機收斂,套用於機率論與數理統計。基本介紹 在機率論中,依機率收斂是隨機變數收斂的方式之一。一個隨機變數序列(Xn)n>=1 依機率收斂到某一個隨機變數 X ,指的是 Xn 和 X 之間存在...
亦稱“隨機收斂”。稱隨機變數列{Xₙ}依機率收斂於隨機變數X, 記作 或 ,如果對於任意 ,有 。以機率1收斂 亦稱幾乎必然收斂。稱隨機變數列X₁,X₂,…,Xₙ,…以機率1收斂於隨機變數X,記作 或 ,如果 ,...
均方收斂(convergence in the mean square)指的是機率論中常用的一種收斂性。公式 均方收斂的公式是 概念 均方收斂,由馬爾科夫不等式可以推出如下不等式:可以得出均方收斂是依機率收斂的充分條件,而根據依機率收斂的定義可以推出:所以...
依機率收斂於 。一般地,設 為一個隨機變數序列,a 是一個常數,若對於任意正數 都有 則稱隨機變數序列 依機率收斂於a 。定理1 表明,當n 很大時,隨機變數 的算術平均 接近於數學期望 ,這種接近是機率意義下的接近。證明方法 這...
第一節 隨機變數序列的四種收斂性 一、依分布收斂 二、依機率收斂 三、以機率1收斂 四、r-階收斂 第二節 大數定律 一、(弱)大數定律 二、強大數定律 第三節 中心極限定理 習題五 第六章 抽樣分布 第一節 總體、樣本和統計...
4.1 依機率收斂 4.2 大數定律 習題4.2 4.3 中心極限定理 習題4.3 總練習題四 第五章 數理統計的基本知識 5.1 數理統計的基本概念 一、總體與樣本 二、樣本的分布函式 三、經驗分布函式 四、統計量 習題5.1 5.2 抽樣...
6.1 依機率收斂與平均收斂 293 6.1.1 依機率收斂 293 6.1.2 平均收斂 299 6.2 依分布收斂 306 6.2.1 依分布收斂的概念 306 6.2.2 連續性定理及其套用 309 6.3 弱大數律和中心極限定理 314 6.3.1 弱大數律 315 6...
當r=1時稱為平均收斂。當r=2時又叫均方收斂。性質 r階收斂可歸納以下幾個性質:性質1 對於0 ξ,則ξ𝚗 ξ。性質2 如果對於某個r>0,隨機變數列ξ₁,ξ₂,……r階收斂於隨機變數ξ,則它一定也依機率收斂於ξ。性...
§5.1 依機率收斂和切比雪夫不等式 一、依機率收斂 二、切比雪夫不等式 §5.2大數定律 一、切比雪夫大數定律 二、伯努利大數定律 三、辛欽大數定律 §5.3 中心極限定理 一、棣莫弗-拉普拉斯定理 二、列維-林德伯格定理 習題五...
強一致性(strong consistency)參數估計的一種收斂性質.指參數估計值以機率為1收斂到參數真值.又稱為強相容性.設丫一(y}l)}y}2),...}y(n>為R”中一隨機向量,B(y0)為有限維參數B的一個估計,若B(yn>}B,當n~二,則B (...
經驗分布是一種函式。經驗分布函式是對產生樣本點的累積分布函式的估計。根據Glivenko-Cantelli定理,它以機率1收斂於潛在的分布。有許多結果可以量化經驗分布函式與基礎累積分布函式的收斂速度。術語介紹 在統計學中,經驗分布函式是與樣本的...
強大數定律可能是機率論中最廣為人知的結果,它表明了獨立同分布的隨機變數序列的均值以機率1收斂到分布的均值。定理1 [強大數定律] 設 為一獨立同分布的隨機變數序列,其公共均值 有限.則下式以機率1成立: 即強大數定律可以表達...
依機率或以機率1收斂於零,則分別稱 是依機率穩定或以機率1穩定的。這是大數律的一種推廣形式。由於 依機率收斂於零與 的分布向集中於零的退化分布弱收斂是等價的,因此弱大數律就是討論 的分布向退化分布弱收斂的極限定理(見中心...
以機率1收斂於θ(見機率論中的收斂),稱 為θ的強相合估計。的這個性質只有在n→ 時才有意義,這叫做大樣本性質,而強相合性的研究屬於大樣本統計的範圍。根據統計量的極限性質而得出的統計方法稱為大樣本方法。例如:設X1,X2,…,Xn...
,在此樣本空間上導出的機率分布序列記為{}。將分布函式序列{}的弱收斂概念加以推廣,可以研究序列{}的弱收斂問題,也可以研究過程樣本函式列以機率1收斂的問題,後者有時也稱為強收斂問題。機率測度弱收斂 用 ε表示度量空間上的波萊爾...
隨機連續性(stochastic continuityin probability)是隨機過程的一種分析性質。如果當t→t₀(t∈T)時,X(t)依機率收斂於X(t₀),則稱隨機過程{X(t),t∈T}在t₀∈T處是隨機連續的。概念 隨機連續性(stochastic continuityin ...
一般來說,RS積分定義中的達布和不會以機率1收斂到一定的極限,但在適當的條件下,達布和的均方極限存在。伊藤清正是利用這一性質定義了對布朗運動的隨機積分。設 t∈R+= 【0,∞)}是一族上升的子σ域,布朗運動W={W(t),t∈...
依機率收斂於 ,即當n充分大時,有 。強相合估計 稱 為 的強相合估計,如果 以機率1收斂於 ,即當n充分大時,有 。r階相合估計 稱 為 的r階相合估計,如果 r階收斂於 ,即當n充分大時,有 。特別,當r=2時,稱 為 的...
收斂到u。如果說“弱大數定律”,上述收斂是指依機率收斂(in probability),如果說“強大數定律”,上述收斂是指幾乎必然收斂(almost surely/with probability one)。大數定律通俗一點來講,就是樣本數量很大的時候,樣本均值和真實均值充...
根據伯努利大數定律,只要n足夠大,Fₙ(x)依機率收斂於總體分布函式F(x)。事實上還可以有更進一步的結論,這就是格利文科(w.Glivenko)定理 按 , ,的圖形,如下圖2,Cₙ,C來講,這定理表明,對於任意給定的ε>0,機率...
幾乎處處收斂與依機率收斂不同。生活例子:開始上課了,慢慢地大家都安靜下來,這是幾乎處處收斂。絕大多數同學都安靜下來,但每一個人都在不同的時間不安靜,這是依機率收斂。還有大數定律在保險業套用也十分廣泛。大數定律又稱大數...
”的機率接近於0,則稱隨機變數序列{Xₙ}依機率收斂於a。正因為是機率,所以不排除小機率事件“”發生。所以,依機率收斂是不確定現象中關於收斂的一種說法,記為 。切比雪夫定理 設X₁,X₂,…,Xₙ,…是相互獨立的隨機...
附錄C 機率論的補充知識 393 C.1 隨機變數的收斂 393 C.1.1 依機率1收斂 393 C.1.2 依機率收斂 395 C.1.3 均方收斂 396 C.1.4 依分布收斂 396 C.2 特徵函式 397 C.3 KL散度與大偏差原理 399 參考文獻...
第3章 各種收斂方式與極限分布 3.1 依機率收斂 3.2 幾乎必然收斂 3.3 r階中心矩收斂 3.4 依分布收斂 3.5 各種收斂方式之間的關係 3.6 漸近理論中的基本工具 3.7 隨機數的產生 3.8 習題 第4章 數據壓縮技術 4....
由於有了具有可列可加性的測度和建立在這種測度基礎上的積分,導致了與微積分中函式序列的點點收斂和一致收斂不同的一些新的重要收斂概念的產生,它們是幾乎處處收斂、度量收斂(亦稱依測度收斂)、積分平均收斂等。度量收斂在機率論中就是...
理論上期望值的計算沒有什麼錯誤,我們需要承認它的期望值是無窮大;而實際上它的均值又不可能是無窮大,因為它是樣本均值,樣本均值隨著樣本容量的增加,以機率收斂於其期望值。這都是正常的,它們本身就是應該有差距的!至於差距應該有...
