基本介紹
介紹,起源,主要內容,意義,學術基礎,
介紹
由於人生保險的標的是人的生命和身體，因此保險事故發生帶來的損失很難用價值標準來衡量。它不同於以物為保險標的的財產保險，物的損失價值是可以估算的。因此，人生保險事故發生時保險人的賠償金額即保險金額一般只能根據投保人的經濟收入、家庭狀況、生活水平和繳費能力等，由保險人和投保人相互協商來確定。
起源
早期的壽險組織其經營的壽險業務有很大的局限，概括起來有以下幾個特點：首先，壽險業務所承保的對象單一，限制較多；其次，業務量小，尚未大規模經營壽險業務；最重要的是，壽險經營缺乏嚴密的科學基礎，表現在考慮的因素較少，有關計算粗糙不精確。在這樣的背景下，造成的是壽險業的不景氣，保險技術的停滯不前。
壽險精算學的產生並不是偶然的，它具有自身的理論淵源。1693年，英國天文學家、數學家埃德蒙·哈雷根據德國Breslan市居民的死亡資料，編制了世界上第一個完整的死亡表，用科學的方法精確地計算出各年齡段人口的死亡率。哈雷在其中對死亡率、生存率以及死亡率隨年齡不同而異等概念的研究，不僅使產生於12世紀的年金價格計算更為精確，也為後來精算的產生奠定了科學的基礎。18世紀中期，托馬斯·辛普森根據哈雷的死亡表構造了依據死亡率變化而變化的保險費率表。後來，詹姆斯·多德森又根據年齡的差異確定了更為精確的保險費率表，進一步為精算奠定了基礎。1724年，法國數學家Abraham de Moivre通過對死亡率及其模型作過的大量研究，提出了一個死亡法則，即將一定年齡對應的生存人數看作這一年齡的函式。Moivre的這一死亡法則成功地計算和簡化了當時棘手的年金問題。這些科學家的工作為壽險精算學的建立作出了重大的貢獻，奠定了其數理基礎。
1756年英國人詹姆斯·道森被以年齡偏大為由拒保，他鑒於此事，提出了保險費應與死亡率相掛鈎，隨投保人的年齡和預期壽命不同而有所差異等新的保險經營理念。這一理念就是現代壽險精算學的雛形。1762年，英國成立了世界上第一家真正的壽險公司——倫敦公平保險公司。該公司採納了道森的方案，以死亡表為依據，採用均衡保費的理論來計算保費，並且對不符合標準的投保人另行收費。壽險經營據此打開了新的局面，同時壽險業務開始步入科學的經營之路。該公司的成立，標誌著現代壽險制度的建立。
主要內容
意義
第一，風險是客觀存在的。一方面，各種自然災害是按自然規律運行的客觀現象，使人力不可抗拒的；另一方面，各種人為事故雖然可以通過加強管理得以減輕，但無論怎樣努力，都只能避免個別事故而不可能從整體上消除事故發生的風險。因而，儘管人們在一定的時間和空間可以發揮主觀能動性改變風險存在和發生的條件，進而降低風險發生的頻率和損失程度，但絕對不可能消滅風險。
第四，風險是可以預測。從現代的機率論和數理統計可知，由於風險是一種損失的隨機不確定性，對於群體來說，各種風險發生的機率、損失的大小及其波動性是可以大致計算出來的。風險的這些特徵表明，在實際的保險經營中，不可避免地存在著一定的風險，同時這些風險又是可以通過科學的方法來預測和減少的。這就要求，在人身保險的經營中必須考慮到這些風險的存在，運用定量的方法進行精確的風險分析。
其次，人身保險經營的特性也決定了其必須要進行大量的定量分析。人身保險的保單一般是長期契約，這就決定了其收入和支出在時間上是不配比的，且為了支付未來賠償而籌集的保費與未來實際發生的賠償金額也存在差別。為了降低經營的風險，就必須把這些差別控制在一定的範圍內並儘量降低，而這就需要科學精確地厘定保險費率，其考慮的主要因素為預估的死亡率、利息率、費用率，它們都是時間隨機變數函式。此外，人身保險經營中收入與支出時間上的不配比也使得經營過程中存在大量的閒置資金，所以人身保險中閒置資金的投資就是一項重要的工作。但投資項目的選擇、投資風險的分析、投資金額的確定、投資回報率的估計、投資績效的評價等都是需要精確確定的，也即與精算有關。
除以上所分析的項目以外，人身保險中需要精算的地方還很多，如隨著時間的變化，生命表應作一定的修正，相應地，原來一定時期內相對穩定的費率也將變化；經濟周期對人身保險的影響及由此引起的經營調整等。總之，人身保險的科學運營客觀上離不開精算，人身保險精算使人身保險的經營科學化，確保了經營的穩定性和盈利水平。
學術基礎
自然界和人類社會發生的現象是各種各樣的。有一類現象，在一定條件下必然發生，可以事先準確的預言其結果。我們把這類現象稱為確定性現象。在我周圍還存在著另一類現象，例如，在相同條件下拋同一枚硬幣，其結果可能是正面朝上，也可能是反面朝上，並且在每次拋擲之前無法肯定拋擲的結果是什麼。這類現象，在一定的條件下，可能出現這樣的結果，也可能出現那樣的結果，而在試驗或觀察之前不能預知確切的結果。但人們經過長期實踐並深入研究之後，發現這類現象在大量重複試驗或觀察下，它們的結果都呈現出某種規律性。例如，多次重複拋擲一枚硬幣，得到正面朝上的次數大致有一半。這種在大量重複試驗或觀察中所呈現出的固有的規律性，就是統計規律性。這種在個別試驗中其結果呈現出不確定性，在大量重複試驗中其結果又具有統計規律性的現象，我們稱之為隨機現象。
在機率論中，是通過隨機試驗來研究隨機現象的。所謂隨機試驗就是符合以下特徵的事件：（1）可以在相同的條件下重複地進行；（2）每次試驗的可能結果不止一個，並且能事先明確實驗的所有可能結果；（3）進行一次試驗之前不能確定那一個結果會出現。對於隨機試驗，儘管在每次試驗之前不能預知試驗的結果，但試驗的所有可能結果組成的集合是已知的。我們將隨機試驗的所有可能結果組成的集合稱為隨機試驗的樣本空間。樣本空間的元素，即隨機試驗的每個結果，稱為樣本點。樣本空間的子集稱為隨機試驗的隨機事件。
在保險的經營中，風險的普遍性、複雜性決定了如果保險人不加選擇地對各種要求風險轉嫁的客戶都承保，就可能使自己陷入經營困境中。因此，保險人通常將風險劃分為可保風險和不可保風險，其中可保風險才是保險人可以承保的風險。而作為可保風險，其發生必須是偶然的，即所承保的保險事故必須是隨機事件。風險發生的偶然性是針對單個風險主體來講，風險的發生與損失程度是不可知的、偶然的。對於必然會發生的事件，如機器設備的折舊和自然損耗，保險人是不予承保的。從前述的知識我們可知，對於單個主體無法預知的風險的發生及損失的大小，保險人可通過大量的統計資料的分析，找出其發生的規律性，從而將偶然的、不可知的風險損失轉化為可預知的費用支出，順利實現保險經營的全過程。
人身保險精算
如果A是一隨機事件，那面它在一次試驗中可能發生，也可能不發生。但僅僅知道這一點對我們的實際工作是沒有多大的幫助的。實際中，人們不僅想知道某一事件的發生是否確定，而更為關心的是，如其可能發生，發生的可能性究竟有多大。例如，把一枚硬幣拋擲1萬次，僅僅知道正面朝上可能發生也可能不發生是遠遠不夠的，更為重要的是應知道這1萬次中正面朝上的次數可能是多少。為此，需要引進機率的概念。
機率表示隨機事件發生的可能性的大小，機率大就表示某種隨機事件出現的可能性就大，反之，機率小則表示某種隨機事件出現的可能性就小。機率是不確定性事件的確定性程度，即衡量隨機事件出現的可能性大小的尺度。假定以P(A)表示隨機事件A發生的機率，由於必然事件E是肯定會發生的，可以約定P (E)=1,同時，由於不可能事件Φ肯定不會發生，可以約定P(Φ)=0,這樣，對於一般的事件A,應有0≤P(A)≤1。
2. 大數定律及其在保險中的套用
前面講到危險事故的發生對於單個主體是隨機的、不可測的，而對社會群體來說則是必然的、可估測的，這即是由大數定律決定的。大數定律是指隨機事件在一次獨立試驗中發生的這種偶然性在大量的重複試驗中將呈現為事件發生髮展的某種必然的規律性。它說明了大量的隨機現象由於偶然性相互抵消所呈現的必然數量規律，是保險經營的重要數理基礎。
大數定律套用於保險時得出的最有意義的結論是：當保險標的的數量足夠大時，通過以往統計數據計算出的估計損失機率與實際機率的誤差將很小。保險經營利用大數定律把不確定的數量關係轉化為確定的數量關係，即某一危險是否發生對某一個保險標的來說是不確定的，可能發生也可能不發生，但當保險標的數量很大時，我們可以很有把握地計算出其中遭受危險事故的保險標的會是多少。這樣，根據大數定律，我們就把對單個保險標的來說不確定的數量關係轉化為了對保險標的的集合來說確定的數量關係。
人身保險中，每個被保險人在一定時期是否發生危險事故是隨機的、不確定的，並且各被保險人之間發生危險事故是相互獨立。當面臨同類危險的被保險人組成被保險集團時，相當於對隨機事件進行多次重複觀察。此時，被保險集團中發生危險事故的頻率將隨著被保險人數的增多而趨於穩定值，這個穩定值就是危險事故發生的機率。因而可以說單個被保險人遭受危險事故的不確定性將在被保險集團中消失，從而表現為，對於社會總體來說，危險事故的發生為確定的機率值，這一機率值也正是被保險人發生危險事故的可能性。因此可以說，雖然單個主體遭受危險事故是隨機的、不可測的，但他遭受危險事故的可能性是可測的、確定的。
保險人把單個被保險人面臨的不確定性的損失轉移到自己身上，也就把不確定的損失轉移為保險人對全體被保險人確定的損失補償金額，也就是說，在一定風險下，保險人承擔的損失補償金額是確定的。另外，保險人為組織和經營保險業務需要有一定的營業費支出，這部分費用是由保險人充分考慮保險經營的市場競爭及實際開支需要的情況下確定的。這樣，保險人為承擔風險的開支總額是可以預先計算的。根據保險人和被保險人權利和義務的對等關係，被保險人想轉嫁風險而需繳納的保險費就可以確定了。通過保險這一方式，投保人實現了分散風險、分攤損失。保險就像是一個蓄水池，每個投保人繳納少量的保費，保險公司把這些資金集中起來以彌補少數被保險人所遭受的損失。
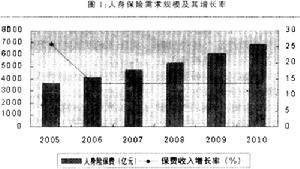人身保險精算