產生原因
第一,
貨幣時間價值是
資源稀缺性的體現。經濟和社會的發展要消耗社會資源,現有的社會資源構成現存社會財富,利用這些社會資源創造出來的將來物質和文化產品構成了將來的社會財富,由於社會資源具有
稀缺性特徵,又能夠帶來更多社會產品,所以現在物品的效用要高於未來物品的效用。在
貨幣經濟條件下,貨幣是商品的價值體現,現在的貨幣用於支配現在的商品,將來的貨幣用於支配將來的商品,所以現在貨幣的價值自然高於未來貨幣的價值。
市場利息率是對平均經濟成長和社會
資源稀缺性的反映,也是衡量
貨幣時間價值的標準。
 資金的時間價值
資金的時間價值第二,貨幣時間價值是
信用貨幣制度下,
流通中貨幣的固有特徵。在目前的信用貨幣制度下,流通中的貨幣是由中央銀行
基礎貨幣和商業銀行體系
派生存款共同構成,由於信用貨幣有增加的趨勢,所以
貨幣貶值、
通貨膨脹成為一種普遍現象,現有貨幣也總是在價值上高於未來貨幣。市場利息率是可貸資金狀況和通貨膨脹水平的反映,反映了貨幣價值隨時間的推移而不斷降低的程度。
第三,貨幣時間價值是人們認知心理的反映。由於人在認識上的局限性,人們總是對現存事物的感知能力較強,而對未來事物的認識較模糊,結果人們存在一種普遍的心理就是比較重視現在而忽視未來,現在的貨幣能夠支配現在商品滿足人們現實需要,而將來貨幣只能支配將來商品滿足人們將來不確定需要,所以現在單位貨幣價值要高於未來單位貨幣的價值,為使人們放棄現在貨幣及其價值,必須付出一定代價,利息率便是這一代價。
資金時間價值表示方法:
表示方法
資金時間價值可以用絕對數表示,也可以用相對數表示,即以利息額或利息率來表示。但是在實際工作中對這兩種表示方法並不做嚴格的區別,通常以利息率進行計量。利息率的實際內容是社會
資金利潤率。各種形式的利息率(
貸款利率、
債券利率等)的水平,就是根據社會資金利潤率確定的。但是,一般的利息率除了包括資金時間價值因素以外,還要包括
風險價值和
通貨膨脹因素。
資金時間價值通常被認為是沒有風險和沒有通貨膨脹條件下的社會
平均利潤率,這是
利潤平均化規律作用的結果。作為資金時間價值表現形態的利息率,應以社會平均資金利潤率為基礎,而又不應高於這種資金利潤率。
 資金的時間價值
資金的時間價值 水利工程案例
資金經合理運用一定時間後,所具有的贏利增值的
潛在能力。利率越高、時間越長,所贏得的利潤及增值也越多,一般以
複利公式加以計算。現在擁有的一定數量的資金,等價於若干年後更大數量的一筆資金;同理,若干年後的一筆資金,折算為現值時要打一折扣。一年後的資金折算為現在的資金時所打的折扣,稱為
折現率。由於水利工程的壽命一般很長,在壽命期內還要確定一個為期30~50年的經濟分析期。在此期中每年都可能投入或回收一定的資金。為了比較各方案的經濟效率,需要將不同年份的資金按其時間價值折算為同一時間的資金值。資金的時間價值
資金流程圖
為了直觀清晰地表達某項水利工程各年投入的費用和取得的收益,可以繪製資金流程圖(圖1)。圖中的橫坐標為時間,每小格表示1年;縱坐標為資金,箭頭長度按一定比例表示資金數值,箭頭向上的為收入,向下的為
支出。一般以工程完工並開始投入運行之年的年初作為原點(基點),原點左邊各年是施工期,原點右邊各年是運行期。為簡便起見,一般都把各年的收支金額當作是集中在年末發生的。從圖上可以很容易看出,第一年的年末就是第二年的年初。
不同時資金的相互折算
根據
複利計算原理對不同年份的資金,可按下列方法進行相互折算。
一次整付折算 資金
P在第一年初開始使用,如
年利率為
i,在使用期中不取出利息,則到
n年末所一次整付的本利和
F值應為:
(1)
式中
P為現值;
F為終值;(1+
i)n為一次整付終值因子並用符號(F/P,i,n)表示。亦即現在的P元,可折算為n年末的P(1+i)n元。 當已知終值F,要折算為
現值P時,可用下式計算:(2)
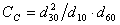 資金的時間價值
資金的時間價值式中為一次整付現值因子,用符號(
P/
F,
i,
n)表示。資金的時間價值
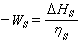 資金的時間價值
資金的時間價值均等
年金折算 如在
n年的每年末均存入一相等的年金
A值(圖2),
年利率為
i,則到
n年末所得本利和
F為:(3)
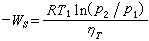 資金的時間價值
資金的時間價值式中為均等
年金本利因子,可用符號(
F/
A,
i,
n)表示。
 資金的時間價值
資金的時間價值如已知
F,要折算為各年年金為
A的
n年均等系列,則可用下式計算:(4)
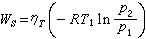 資金的時間價值
資金的時間價值式中為
償債基金因子,用(
A/
F,
i,
n)表示。其含意為如某人擬在
n年末償還1元的債務,當年利率為
i時,應在
n年中的每年末支付(
A/
F,
i,
n)金額。
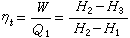 資金的時間價值
資金的時間價值將均等
年金系列換算為相應的現值
P時,可用下式:(5)
 資金的時間價值
資金的時間價值式中為均等年金現值因子, 用(
P/
A,
i,
n)表示。其含意是,如在
n年中的每年末要提取1元錢,且
年利率為
i時,在開始時應投入的資金數值。
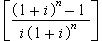 資金的時間價值
資金的時間價值將現值
P換算為等價的均等
年金系列時,可用下式:(6)
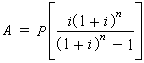 資金的時間價值
資金的時間價值式中為
資本回收因子,用符號 (
A/
P,
i,
n)表示。其含意為開始投入1元錢,當利率為
i時,在
n年的每年末可以提取的錢數。資金的時間價值
 資金的時間價值
資金的時間價值遞增等差
年金折算 如在
n年內每年年末的收入不是均等的,而是隨著工程的逐漸完善而成等差級數遞增的,就成為一個遞增等差年金系列(圖3)。在第一年末收支的金額為0,第二年末的金額為
G,第3年末的金額為2
G,如此類推,在
Π年末的金額為(
n-1)
G,各年的級差為
G。
這一遞增等差年金系列可按下式折算成現值
P:(7)
 資金的時間價值
資金的時間價值也可按下式折算為均等
年金系列的
A:(8)
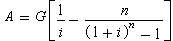 資金的時間價值
資金的時間價值式中為遞增
轉換因子,用符號(
A/
G,
i,
n)表示。用此因子將遞增等差
年金系列轉換成一個均等年金系列後,即可利用上面的(3)(4)(5)(6)各式,進行資金的各種折算。
 資金的時間價值
資金的時間價值複利因子表
上列公式(1)(2)(3)(4)(5)(6)(8)中的各種複利因子,均已按不同的利率i和年數n,製成複利因子表(見表),加以查用,可使計算十分簡捷。資金的時間價值
水利工程壽命
①物理壽命:從水利工程或某項設施建成至不能使用為止的一個期限,又稱實際壽命。
②經濟壽命:從某項水利工程或設施投入使用起,至一定年數後,由於效益降低、運行維修費用增加或高效能新產品的問世,以致再繼續使用原設施不如重新建造或購置更新,更為經濟。這時,這種設施的經濟壽命就結束了。隨著科學技術的進步,同等效能設施的建造費和運行維修費往往比以前降低,因此經濟壽命就會縮短。不易損壞的耐用建築物的經濟壽命很長,而機電設備的經濟壽命一般較短。可根據更新重置的經濟分析,對水利工程的經濟壽命加以確定。
經濟分析期
在工程的經濟壽命期內,選定一個期限作為各方案共同的經濟分析期。這一期限應有足夠的長度,使各方案的有利和不利的經濟、環境和社會方面的效果均能充分顯示出來,並達到相對穩定的程度,從而使各方案之間具有比較一致的可比條件。
一般大型水利工程的經濟分析期可以採用50年。如果某一方案的經濟壽命短於共同的經濟分析期時,則可以在它的壽命終了時進行更新重置,以便與經濟壽命較長的方案進行比較。如果某工程方案的經濟壽命長於經濟分析期,則應計算該方案在經濟分析期終了時所保有的殘值。
影響因素
1、資金的使用時間。在單位資金和利率(或利息,i >0現實中利率或利息總是大於0)一定的條件下,資金使用時間越長,則資金的時間價值越大;反之,資金使用時間越短,則資金的時間價值越小。
2、資金數量的多少。在單位時間和利率(或利息,i >0現實中利率或利息總是大於0)一定的條件下,資金數量越大,資金的時間價值就越大;反之,資金的數量越小,資金的時間價值就越小。
3、資金投入和回收的特點。在總投入資金一定的情況下,前期投入的資金越多,資金的時間價值越小;反之,後期投入的資金越多,資金的時間價值越大。在資金回收額一定的情況下,前期回收的資金越多,資金的時間價值越大;反之,後期回收的資金越多,資金的時間價值小。
4、資金周轉的速度。在單位時間、單位資金和利率(或利息,i >0現實中利率或利息總是大於0)一定的條件下,資金周轉的越快,資金的時間價值越大;反之,資金周轉的越慢,資金的時間價值越小。
 資金的時間價值
資金的時間價值 資金的時間價值
資金的時間價值
 資金的時間價值
資金的時間價值 資金的時間價值
資金的時間價值 資金的時間價值
資金的時間價值 資金的時間價值
資金的時間價值 資金的時間價值
資金的時間價值 資金的時間價值
資金的時間價值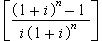 資金的時間價值
資金的時間價值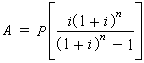 資金的時間價值
資金的時間價值 資金的時間價值
資金的時間價值 資金的時間價值
資金的時間價值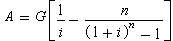 資金的時間價值
資金的時間價值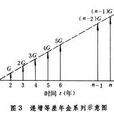
 資金的時間價值
資金的時間價值 資金的時間價值
資金的時間價值
 資金的時間價值
資金的時間價值 資金的時間價值
資金的時間價值 資金的時間價值
資金的時間價值 資金的時間價值
資金的時間價值 資金的時間價值
資金的時間價值 資金的時間價值
資金的時間價值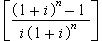 資金的時間價值
資金的時間價值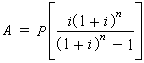 資金的時間價值
資金的時間價值 資金的時間價值
資金的時間價值 資金的時間價值
資金的時間價值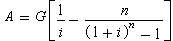 資金的時間價值
資金的時間價值