基本介紹
- 中文名:三角比
- 外文名:trigonometric ratio
- 別稱:三角學
- 學科:幾何
概述
 圖1.三角比
圖1.三角比


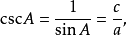

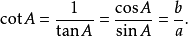
相關定義及公式
銳角三角比的定義
同角的三角比關係
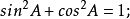

互為餘角的三角比關係
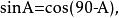
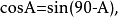
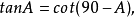

直角三角形邊、角關係
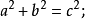

誘導公式
公式一
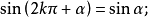
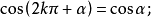
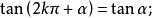
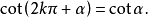
公式二
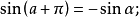
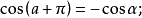


公式三
公式四

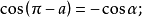
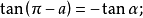
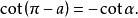

 圖1.三角比
圖1.三角比


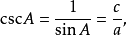

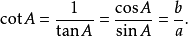
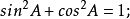

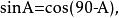
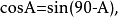
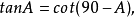

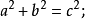

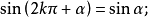
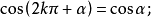
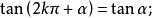
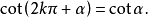
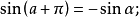
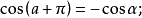



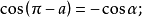
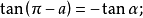
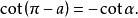
三角比(trigonometric ratio)是三角學的基本概念之一,指三角函式定義中的兩線段的數量比。 定義銳角三角函式時,是指含此銳角的直角三角形中任意兩邊的比。定義任意...
銳角三角比(trigonometric ratio)是指一個銳角的正切、餘切、正弦、餘弦的統稱。三角比是三角學的基本概念之一,指三角函式定義中的兩線段的數量比。...
三角函式是基本初等函式之一,是以角度(數學上最常用弧度制,下同)為自變數,角度對應任意角終邊與單位圓交點坐標或其比值為因變數的函式。也可以等價地用與單位圓有...
又稱三角函式的加法定理,是幾個角的和(差)的三角函式通過其中各個角的三角函式來表示的關係...
三角函式關係編輯 鎖定 倒數關係: sina*csca=1 cosa*seca=1 tana*cota=1 商數關係: tana=sina/cosa cota=cosa/sina 平方關係: (sina)^2+(cosa)^2=1 1...
三角函式是基本初等函式之一,是以角度(數學上最常用弧度制,下同)為自變數,角度對應任意角終邊與單位圓交點坐標或其比值為因變數的函式。也可以等價地用與單位圓有...
所謂三角函式的通式,也就是三角函式的一般表達式。...... 所謂三角函式的通式,也就是三角函式的一般表達式。目錄 1 通式的表達式 2 物理意義 3 例題選析 三角...
三角函式是數學中屬於初等函式中的超越函式的函式。它們的本質是任何角的集合與一個比值的集合的變數之間的映射。通常的三角函式是在平面直角坐標系中定義的。其定義...
三角函式六邊形記憶法(Mnemonics in trigonometry)是一通過六邊形進行記憶三角函式運算規則的計算方法。其特徵為“上弦中切下割,左正右餘1中間。”...
毛羅利科早於1558年已採用三角函式符號(Signs for trigonometric functions), 但當時並無函式概念,於是只稱作三角線( trigonometric lines)。他以sinus 1m arcus 表示...
餘弦(餘弦函式),三角函式的一種。在Rt△ABC(直角三角形)中,∠C=90°(如圖所示),∠A的餘弦是它的鄰邊比三角形的斜邊,即cosA=b/c,也可寫為cosa=AC/AB。...
一般指含有某些三角函式的方程,這些三角函式的自變數中含有未知數,含有未知數的三角函式的方程叫做三角方程。適合於方程的一個未知數的實數值(可以理解為角的弧度數)...
要做到能夠十分靈活地運用三角函式,微分、積分、複數等一些相關知識必不可少。如果通過《三角函式超入門》的學習,不僅能使讀者掌握三角比、三角函式的相關公式,還能...
高中數學必修四第一章(三角函式)第二節內容。...... 在直角坐標系中,⊙O的半徑為1,任意角α的三角函式定義如下:正弦∠α與單位圓的交點A的縱坐標與圓半徑的...
《三角函式》是GNZ48 TEAM Z第一套原創公演,也是GNZ48的第三套原創公演。...... 《三角函式》是GNZ48 TEAM Z第一套原創公演,也是GNZ48的第三套原創公演。 [...
三角函式的基礎是平面幾何中的相似形與圓,但研究的方法是採用代數中函式的研究方法和代數運算的方法,於是使三角函式成了聯繫幾何和代數的橋樑,使它在幾何和代數中...
在數學中,傅立葉級數是一種三角級數,傅立葉級數也常稱為三角級數。但並不是所有三角級數都是傅立葉級數。一個有趣的問題是給定一個三角級數,當x取什麼值時...
倍角公式,是三角函式中非常實用的一類公式。就是把二倍角的三角函式用本角的三角函式表示出來。在計算中可以用來化簡計算式、減少求三角函式的次數,在工程中也有...
和差化積公式:包括正弦、餘弦、正切和餘切的和差化積公式,是三角函式中的一組恆等式,和差化積公式共10組。在套用和差化積時,必須是一次同名(正切和餘切除外)...
