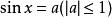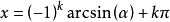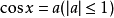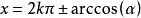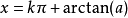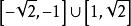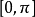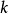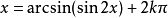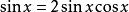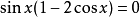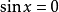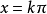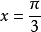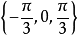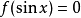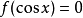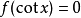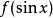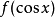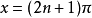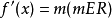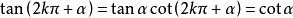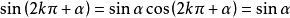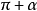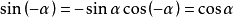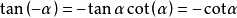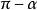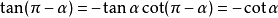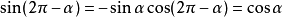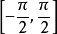定義
一般指含有某些三角函式的方程,這些三角函式的
自變數中含有未知數,含有未知數的三角函式的
方程叫做三角方程。
三角方程是三角中的重要內容,在解三角方程過程中,運用的知識比較廣泛,不僅要用到三角中的許多定理與公式,還要涉及
代數式的變形與
代數方程等
代數知識,最簡單的三角方程實際上是由某角的
三角函式值求角問題的延伸,是
三角函式的周期性和
反三角函式概念的最直接運用。
解題方法
套用通解公式
把一般的三角方程轉化為最簡單的三角方程,其中要套用到三角函式性質及圖像、反三角函式、誘導公式等知識。
一是要掌握其基本方法,要熟悉同名三角函式相等時角度之間的關係在解三角方程中的作用;會用數形結合的思想和 函式思想進行含有參數的三角方程的解的情況和討論。通過解三角方程,可以進一步理解三角函式及反三角函式,進一步提高三角變換能力。
二是要合理選用公式和變換方法。
基本轉化方法
(1)化為同角、同名的三角函式;
(2) 因式分解法;
(4)引入輔助角;
(5)利用三角函式定義求解;
(6)利用比例性質;
(7)利用升降次法;
(8)利用 換元法;
(9)利用萬能置換法。
通過解三角方程,進一步理解三角函式及反三角函式,進一步提高三角變換能力。
基本三角方程的通解
三角方程舉例
首先,明確一下
反正弦函式:
表示一個在
範圍內的角,且其
正弦值為
(
在
),即
例如,形如
或者
或者
或者
的方程,這裡ƒ是有理函式,可用一種
萬能公式,令
或者
或者
或者
然後用這個代入原
方程,即可得到關於t的
有理方程。用這個萬能方法,可以求出除了形如
以外的方程的所有解。不能用精確解法來解的三角方程,可以用近似方法求解。
最簡三角方程
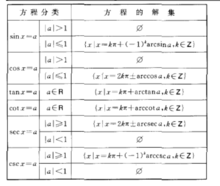
亦稱基本三角方程.含有未知角的基本三角方程。若f(二)是基本三角函式,則
稱為最簡三角方程.凡能用初等方法求解的三角方程,一般都可以通過恆等變換或代數方法歸結為解一個或幾個這樣的最簡三角方程,它們的解集的交或並就是原方程的解.現將這些最簡三角方程的解集列表如下:
三角公式
公式一:
設α為任意角,終邊相同的角的同一三角函式的值相等:
公式二:
設α為任意角,
的三角函式值與α的三角函式值之間的關係:
公式三:
任意角α與-α的三角函式值之間的關係:
公式四:
利用公式二和公式三可以得到
與α的三角函式值之間的關係:
公式五:
利用公式-和公式三可以得到
與α的三角函式值之間的關係: