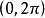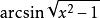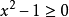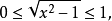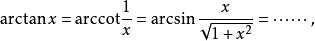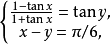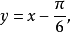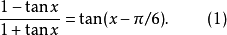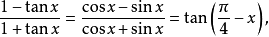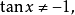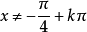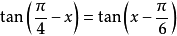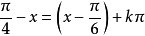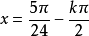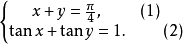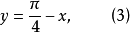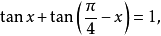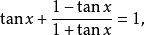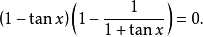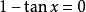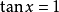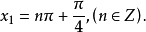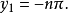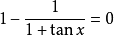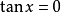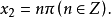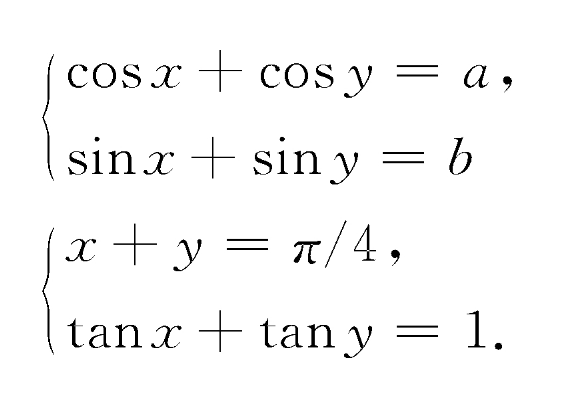三角方程組

所謂三角方程組(system of trigonometric equations)是指方程組中或僅僅包含三角方程，或包含三角方程和代數方程。如果一個未知數能表示為另一個未知數的顯式，那么可將三角方程組化為含單變數的一個方程。有些三角方程組，可根據三角式的恆等變換而化為代數方程組。

基本介紹

• 中文名：三角方程組
• 外文名：system of trigonometric equations
• 所屬學科：數學
• 所屬問題：代數與方程（三角方程）
• 簡介：含有三角方程的方程組

三角函式方程組的解法原理

三角函式方程組的解法原理，與代數學中解方程組的方法類似：它們都是首先通過代數的或三角的變換， 逐漸消去未知數，直到化為含有唯一的未知量的普通方程並對它求解，然後再把這個解代入到其他各式中，求其全部解。

解三角方程組的注意事項

解三角方程組時要注意以下四點：

1. 消去三角方程組中的未知數，一般除了使用代入法外，還常常利用各種三角公式與代數變換。 特別地， 當問題有不同情況時，也常要求有不同的方法，這些並沒有固定的規律可循，這是求解三角方程組的一個很大困難，克服這個圖難的辦法，要求三角公式運用熟練，多作題目，多見類型，逐步提高分析問題的能力。

2. 求得方程組的解之後，與代數中解方程組一樣， 也得一組一組地把解分別列出，並將所得的每組解一一代入到原方程組中進行檢驗，去掉增加根，並要注意遺根。代入檢驗是很麻煩的，一般方法是只把在區間上的角代入進行檢驗，而不把解的一般形式代入到方程組中，這樣可使計算簡單些。

3. 所求得的解，有時還要求受到一定條件的約束，常見的情況有:

(1)當解中含有形如arcsin2或arcsin(-2)這樣的項時，由於這樣的項不可能代表任何確定的角，故應在說明之後捨去。

(2)當解中含有形如的項時，由於我們只在實數範圍內討論三角函式，顯然必須滿足條件

且

並由此求得x的取值範圍。但是， 我們約定，只要題目中沒有明確提出要求，我們並不進行討論，即認為這樣已經求得了最後結果。

4. 由於

所以， 當方程的係數為文字係數時，方程組解的形式往往隨所採取的解法不同而有不同。但是，不管解的形式怎樣，只要合理就行，並不需要化為一致。當方程的係數為普通數字時，我們也這樣辦，但遇到這種情況的機會要少一些。

例題解析

1.解方程組：

解：顯然

且

因為

（即），所以，從方程（1）得，由此，

和。

2.解方程組：

解:由（1）得

使（3）代入（2）

所以

使，則，所以

代入（3）

使，則，所以

代入（3），有

答：方程組的解為