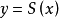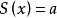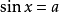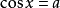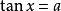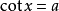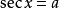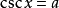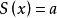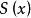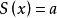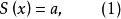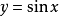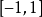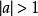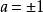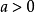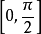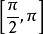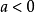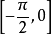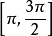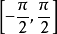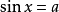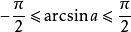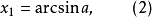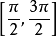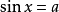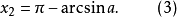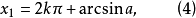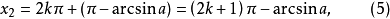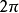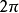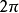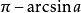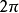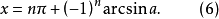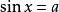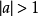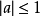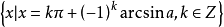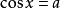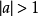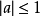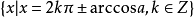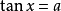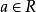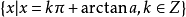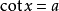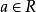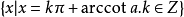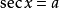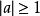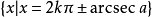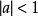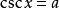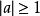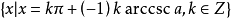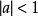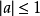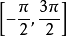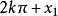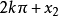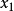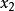最簡三角方程(simplest trigonometric equation)亦稱基本三角方程，是指含有未知角的基本三角方程，若f(x)是基本三角函式，則f(x)=m(m∈R)稱為最簡三角方程，凡能用初等方法求解的三角方程，一般都可以通過恆等變換或代數方法歸結為解一個或幾個這樣的最簡三角方程，它們的解集的交或並就是原方程的解。
基本介紹
- 中文名：最簡三角方程
- 外文名：simplest trigonometric equation
- 所屬學科：數學
- 所屬問題：代數與方程（三角函式）
- 別稱：基本三角方程
基本概念,求解最簡三角方程,最簡三角方程的解集列表,
基本概念
設
是x的基本三角函式，我們稱方程
求解最簡三角方程
求解最簡三角方程
，就是由函式值a來求出函式
相應自變數的一切值。由於基本三角函式S(x)是周期函式，故可先考慮在一個周期內的對應a的一切x值，再加上周期的整數倍，即得滿足 的一切x值。
我們先來討論最簡三角方程
顯然，根據正弦函式
的值域為
，故而，當
時，方程(1)無解。
在單位圓中，正弦線等於a的角一般有兩個(當
時，看成該兩角相重)：當
時，這兩角分別在
和
中；當
時，這兩角分別在
和
中，見圖1。
我們知道，在
中，
有一個解，可用反三角函式來表示:因
，其中
，故
隨著k取一切整數值，(4)和(5)包含了方程(1)的一切解。在方程(1)的無窮多個解中，可看成是或與
關於
同餘(即被 除得的餘數相同，或說成方程的解與 相差 的整倍數)，或與
關於 同餘。我們稱(4)和(5)為方程(1)的通解。
一般說來，一個三角方程雖有無窮多個解，但互不同餘的解之個數是有限的、要求出三角方程的通解，就須求出有限組互不同餘的解。
在通解(4)、(5)中，注意到π前面係數的奇、偶性和式中的+、－號關係，可把(4)、(5) 兩式統一寫成
最簡三角方程的解集列表
循著以上同樣的思想方法，可求得各個最簡三角方程的解，最簡三角方程的解集列表如下：
方程分類 | 方 程 的 解集 | |
 |  | ∅ |
 |  | |
 | | ∅ |
|  | |
 |  |  |
 | |  |
 |  |  |
 | ∅ | |
 | |  |
| ∅ | |
