基本介紹
- 中文名:三角函式恆等變換
- 外文名:Trigonometric function identical deformation
- 套用學科:數學
- 適用領域範圍:三角函式
同角三角函式間的基本關係式:
平方關係

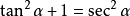
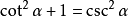
積的關係
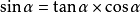





倒數關係



直角三角形ABC中
說明



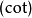


兩角和與差的三角函式


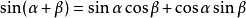



輔助角公式
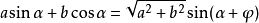


倍角公式



三倍角公式
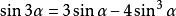
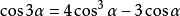
半角公式

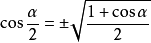

降冪公式



萬能公式



積化和差公式
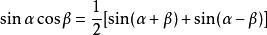
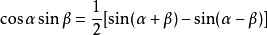


和差化積公式




其他
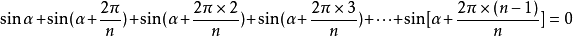
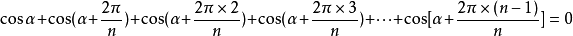




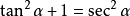
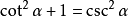
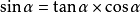











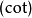




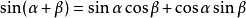



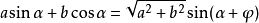





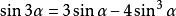
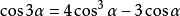

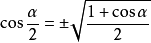







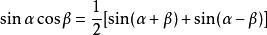
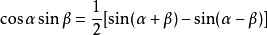






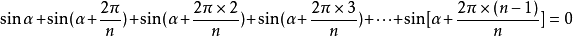
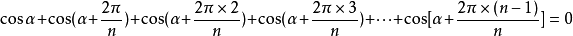


三角函式恆等變形編輯 鎖定 討論999 三角函式的基礎是平面幾何中的相似形與圓,但研究的方法是採用代數中函式的研究方法和代數運算的方法,於是使三角函式成了聯繫幾何...
基本可以從三角函式圖像中推出誘導公式,也能從誘導公式中延展出其他的公式,其中包括倍角公式,和差化積,萬能公式等。中文名 三角恆等變換 外文名 Angle ...
不同的三角函式之間的關係可以通過幾何直觀或者計算得出,稱為三角恆等式。 三角函式一般用於計算三角形中未知長度的邊和未知的角度,在導航、工程學以及物理學方面都...
與以往的三角恆等變換學習相比較,“標準”強調了用向量方法推導差角的餘弦公式,以用三角函式之間的關係推導和(差)角公式、二倍角公式,其他公式(積化和差、和差...
三角函式恆等變形公式·兩角和與差的三角函式:cos(α+β)=cosα·cosβ-sinα·sinβcos(α-β)=cosα·cosβ+sinα·sinβ...
不同的三角函式之間的關係可以通過幾何直觀或者計算得出,稱為三角恆等式。 三角...變化規律正弦值在 隨角度增大(減小)而增大(減小),在 隨角度增大(減小)而減小...
餘弦(餘弦函式),三角函式的一種。在Rt△ABC(直角三角形)中,∠C=90°(如圖...3 三角恆等變換 ▪ 二倍角公式 ▪ 三倍角公式 ▪ 半角公式 ▪...
解反三角方程的根本方法是把方程兩邊同取某一三角函式的三角運算,使它轉化為...利用解代數方程的知識:三角式的恆等變形和換元法等,求得三角方程和反三角方程...
亦稱基本三角方程.含有未知角的基本三角方程。若f(二)是基本三角函式,則 稱為最簡三角方程.凡能用初等方法求解的三角方程,一般都可以通過恆等變換或代數方法歸結...
正切恆等變形公式 兩角和與差的三角函式:cos(α+β)=cosα·cosβ-sinα·sinβcos(α-β)=cosα·cosβ+sinα·sinβsin(α±β)=sinα·cosβ±cosα...
兩角和(差)公式包括兩角和差的正弦公式、兩角和差的餘弦公式、兩角和差的正切公式。兩角和與差的公式是三角函式恆等變換的基礎,其他三角函式公式都是在此公式基礎...
▪ 三角函式 ▪ 正弦函式 ▪ 特定正弦函式與橢圓的關係 2 單位圓 3 級數 4 微分方程 5 指數 6 正弦積分 7 恆等變換 8 數學術語 正弦...
該公式的主要作用是將多個三角函式的和化成單個函式,以此來求解有關最值問題。...注:這種幾何意義同樣適合推導誘導公式等部分三角函式恆等變換公式,但三角函式間...
