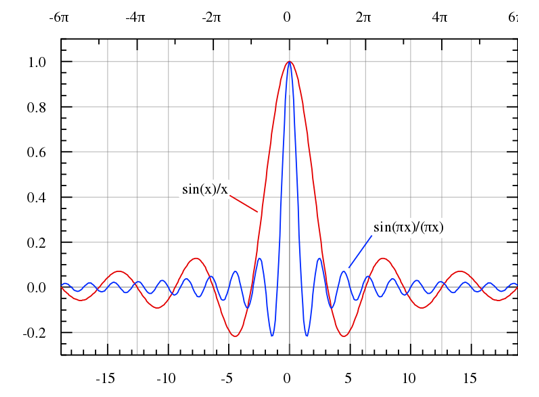
sinc（音同“sink”）濾波器是由sinc函式構造的濾波器。sinc函式的定義可以參考抽樣信號Sa的定義，這裡只需知道矩形脈衝和sinc函式是一個變換對。當矩形脈衝的頻譜沒有混疊時，它就是sin(x)/x,一個sinc函式，對於連續信號，矩形脈衝和sinc函式是傅立葉變換對。對於離散信號這僅僅是一個近似，由於混疊造成了誤差。
基本介紹
- 中文名：sinc濾波器
- 外文名：sinc filter
- 學科：數學、通信
- 套用：信號處理
前提,定義,套用,
前提
sinc函式，又稱辛格函式，用sinc(x)表示。（sinc函式與Sa函式的數學表達形式相同，Sa函式稱為採樣函式，或抽樣函式，用Sa(x)表示，Sa函式詞條請看抽樣信號。）有兩個定義，有時區分為歸一化sinc函式和非歸一化的sinc函式。
在數學領域，非歸一化sinc函式 (for sinus cardinalis)定義為：
sinc函式
定義
在信號處理領域，理想低通濾波器是指一個全部除去給定頻寬之上的信號分量而只保留低頻信號的理想電子濾波器。在頻域它的形狀像一個矩形函式，在時域它的形狀像一個Sinc函式。由於理想的低通濾波器（人們熟知的矩形濾波器）有無限的延遲，所以現實世界中的濾波器只能是它的一個近似，但是它仍然在概念演示或者驗證中得到了廣泛套用，如採樣定理以及Whittaker–Shannon插值公式。
從數學的角度來看，所得到的頻率回響是矩形函式：
其中B是一剪下頻率，即頻寬。這個濾波器的脈衝回響用逆傅立葉變換表示為：
套用
sinc濾波器常見的套用是抗混疊技術。由於高解析度下的來源信號或連續的類比信號能夠存儲較多的數據，但在透過取樣（sampling）時將較多的數據以較少的數據點代替，部分的數據被忽略造成取樣結果有損，當機器把取樣後的數位訊號轉換為人類可辨別的類比信號時造成彼此交疊且有損，在聲音中，便會出現刺耳、不和諧的音調或是噪音。同樣，在3D繪圖時，每個圖形由像素組成，每段瞬間畫面由幀組成，因為螢幕上的像素有限，如果要表現出多邊形的位置時，因技術所限，使用絕對坐標定位法是無法做到的，只能使用在近似位置採樣來進行相對定位。由於沒有足夠的採樣來表現出3D世界中的所有物品的圖形，所以在最後圖像顯示上，這些現象便會造成在物品與物品中過渡的邊緣就會產生波浪狀、圓形、鋸齒和閃爍等有損現象，嚴重影響了畫面的質量。在這種情況下，sinc濾波器就會被套用，用於柔化被混疊上午數位訊號。
