n維射影變換(n-dimensional projective transformation)亦稱n維直射對應,是一類n維變換。指Pn中的一一對應。
基本介紹
- 中文名:n維射影變換
- 外文名:n-dimensional projective transformation
- 所屬學科:數學
- 別名:n維直射對應
- 所屬問題:高等幾何(射影幾何)
基本介紹




相關定理








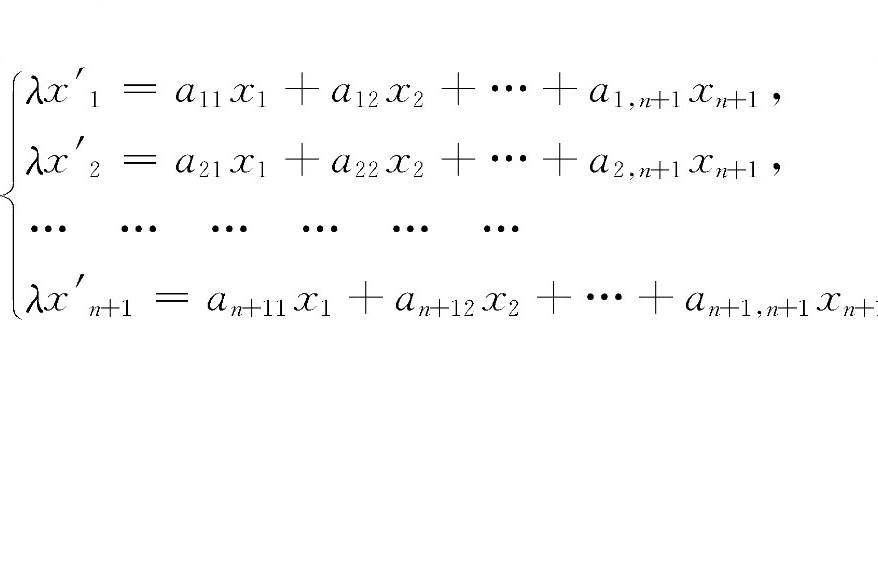
n維射影變換(n-dimensional projective transformation)亦稱n維直射對應,是一類n維變換。指Pn中的一一對應。












n維對射變換(n-dimensional correlation)一類n維變換.指n維射影空間中的點(二)和超平面(u')之間的對應.P”中的對射變換方程可寫為 其中川u;;l}o.當(介紹 n維對射變換(n-dimensional correlation)一類n維變換.指n維射影空間中的點(二...
射影變換群(projective transformation group),簡稱射影群。是一類基本的變換群,即由射影空間中全體射影變換所構成的變換群。變換群是幾何學研究的重要對象。即由變換構成的群。設G是集合S的一一變換所構成的集合,若它滿足:1.集合內任...
若經過一系列的投影和截影,從一個一維基本形到另一個,這兩個基本形就叫做射影相關,它們元素間的對應關係就叫做射影對應。一個射影對應所包含的兩個變換叫做射影變換,它們互為逆變換。在空間,通過投影和截影,點場和線把之間,線...
因此n維(實)射影空間同構於(R-{0})/R.進一步的研究表明P是緊緻解析流形。若令U(0≤i≤n)為P中坐標X≠0的點全體,則UR,且U₀,U₁,…,Uₙ組成P的一個開覆蓋。上述構造方法可以推廣到任意體K上,建立K上的n維射影...
因此n維(實)射影空間同構於(R-{0})/R.進一步的研究表明P是緊緻解析流形。若令U(0≤i≤n)為P中坐標X≠0的點全體,則UR,且U₀,U₁,…,Uₙ組成P的一個開覆蓋。上述構造方法可以推廣到任意體K上,建立K上的n維射影...
復射影空間是實射影空間的推廣,即復歐幾里得空間添加無窮遠點構成的空間。添加了無窮遠點的複平面稱為一維復射影空間,記為 ,推廣到n維,便得到n維復射影空間,其具體構作如下:給定n+1維復歐氏空間C,考慮子集合C\{0}。在其中引進...
射影表示是與相應射影線性群密切相關的一種表示。當K為特徵0的代數封閉域時,有限群G的不可約射影示的次數為G的階的因子。定義 設G為一個群,K為域,n為正整數。把K上n維線性空間V的全線性群記作GL(V)。G 到GL(V)的映射P...
上n維仿射空間 的一點緊化為 上射影空間 。等價地,把n維球面Sⁿ所有對徑點分別粘合起來, 得到的幾何物體稱為射影空間。它的維數就是n。性質 n維射影空間是最簡單的不可定向的單連通緊流形(n為偶數時不可定向,奇數時可定向),...
黎曼流形的變換群是黎曼流形上的具有特殊性質的各種變換群,其中最重要的是等距變換群(又稱運動群)、射影變換群和共形變換群。解釋說明 黎曼流形上的具有特殊性質的各種變換群,其中最重要的是等距變換群(又稱運動群)、射影變換群和...
11.1 仿射變換 11.2 仿射幾何的基本定理 11.3 平面上的仿射變換 第十二章 平面射影變換 12.1 二維射影變換 12.2 變換的層次 12.3 二次曲線的變換及其度量性質 第十三章 三維空間中射影變換 13.1 n維空間中的射影變換 13.2 ...
為冪等變換,或射影變換;若a'一0,則稱Q為冪零變換;若Q>n = E,則稱。為
1.集合內任二變換之積仍屬於這集合;2.集合內任一變換的逆變換仍屬於這集合,則稱G為S的一個變換群。例如,平面上正交變換的全體構成的變換群稱為正交群;平面上仿射變換的全體構成的變換群稱為仿射群。平面上射影變換的全體構成的...
第三種是以蘇步青為首的中國學者開創和發展的結構式射影微分幾何方法,主要是用幾何作圖法來建立射影協變的構圖和不變數。例如用平面曲線在其某種奇點的不變數來表達其他的幾何不變數。共軛網 共軛網是射影曲面論的重要概念之一。n維射影...
就是所求的不變數,這說明不變數個數不超過2n-8個。顯然,這種估算不變數個數的方法可以推廣到n維空間。若幾何元素由k個獨立參數描述,對n維射影變換應有 個獨立參數,當 時應有 個不變數。上面這種不變數個數的估計是不準確的...
在n維實射影空間Pⁿ中,取射影坐標,考慮Pⁿ內的二次曲面 設使Q變為自身的Pⁿ的射影變換的全體所構成的群為G,稱Q為絕對形(absolute),G稱為契約變換群(congruent transformation group)。當a 是雙曲幾何,Hⁿ稱為n維雙...
第1章 n維空間的射影幾何 1.1 射影空間Sn及其線性子空間 1.2 射影結合定理 1.3 對偶原理.進一步的概念.交比 1.4 多重射影空間.仿射空間 1.5 射影變換 1.6 退化的射影變換.射影變換的分類 1.7 Pliicker Sm-坐標 1.8 對射...
n維連通黎曼流形M到自身的共形變換構成的群稱為M的共形變換群,當n≥3時它是維數至多為(n+1)(n+2)/2的李群,n維球面的共形變換群達到了這個最大維數。若黎曼流形M到自身的可微同胚把測地線變為測地線,則稱它為M的一個射影變...
則這個一一對應叫做點場的射影變換,簡稱射影變換。仿射幾何 幾何學的一個分支學科。主要研究仿射空間中的圖形在仿射對應(仿射變換)下不變的幾何性質和不變數。如共線性、平行性和單比等。n維仿射空間的構成如下:設V是一個n維向量空間...
第1章 n維空間的射影幾何 1.1 射影空間Sn及其線性子空間 1.2 射影結合定理 1.3 對偶原理·進一步的概念.交比 1.4 多重射影空間·仿射空間 1.5 射影變換 1.6 退化的射影變換.射影變換的分類 1.7 Pliicker Sm—坐標 1.8 ...
第1章 n維空間的射影幾何 1.1 射影空間Sn及其線性子空間 1.2 射影結合定理 1.3 對偶原理.進一步的概念.交比 1.4 多重射影空間.仿射空間 1.5 射影變換 1.6 退化的射影變換.射影變換的分類 1.7 Pliicker Sm-坐標 1.8 對射...
該原理也可推廣到n維射影空間中去。產生 柏斯卡著名的“神秘的六邊形”定理和布里安昌定理都具有對偶關係,其中前一定理是帕斯卡在1640年於其標題為《略論圓錐曲線》的一張大幅印刷品中公布的;而後一定理則是在1806年由巴黎高等工藝學院...
超曲面(英語:hypersurface)是幾何中超平面概念的一種推廣。假設存在一個n維流形M,則M的任一(n-1)維子流形即是一個超曲面。或者可以說,超曲面的余維數為1。在代數幾何中,超曲面是指n維射影空間上的一個(n-1)維的代數集。
