最大期望算法（Expectation-Maximization algorithm, EM），或Dempster-Laird-Rubin算法，是一類通過疊代進行極大似然估計（Maximum Likelihood Estimation, MLE）的最佳化算法，通常作為牛頓疊代法（Newton-Raphson method）的替代用於對包含隱變數（latent variable）或缺失數據（incomplete-data）的機率模型進行參數估計。
EM算法的標準計算框架由E步（Expectation-step）和M步（Maximization step）交替組成，算法的收斂性可以確保疊代至少逼近局部極大值。EM算法是MM算法（Minorize-Maximization algorithm）的特例之一，有多個改進版本，包括使用了貝葉斯推斷的EM算法、EM梯度算法、廣義EM算法等。
由於疊代規則容易實現並可以靈活考慮隱變數，EM算法被廣泛套用於處理數據的缺測值，以及很多機器學習（machine learning）算法，包括高斯混合模型（Gaussian Mixture Model, GMM）和隱馬爾可夫模型（Hidden Markov Model, HMM）的參數估計。
基本介紹
- 中文名：最大期望算法
- 外文名：Expectation Maximization algorithm, EM
- 類型：最佳化算法
- 提出者：Arthur Dempster，Nan Laird，
- 自定義：Donald Rubin 等
- 提出時間：1977年
- 套用：數據分析，機器學習
歷史,理論,算法,標準算法,改進算法,性質,套用,
歷史
對EM算法的研究起源於統計學的誤差分析（error analysis）問題。1886年，美國數學家Simon Newcomb在使用高斯混合模型（Gaussian Mixture Model, GMM）解釋觀測誤差的長尾效應時提出了類似EM算法的疊代求解技術。在極大似然估計（Maximum Likelihood Estimation, MLE）方法出現後，英國學者Anderson McKendrick在1926年發展了Newcomb的理論並在醫學樣本中進行了套用。1956年，Michael Healy和Michael Westmacott提出了統計學試驗中估計缺失數據的疊代方法，該方法被認為是EM算法的一個特例。1970年，B. J. N. Blight使用MLE對指數族分布的I型刪失數據（Type I censored data）進行了討論。Rolf Sundberg在1971至1974年進一步發展了指數族分布樣本的MLE並給出了疊代計算的完整推導。
EM算法的正式提出來自美國數學家Arthur Dempster、Nan Laird和Donald Rubin，其在1977年發表的研究對先前出現的作為特例的EM算法進行了總結並給出了標準算法的計算步驟，EM算法也由此被稱為Dempster-Laird-Rubin算法。1983年，美國數學家吳建福（C.F. Jeff Wu）給出了EM算法在指數族分布以外的收斂性證明。
此外，在二十世紀60-70年代對隱馬爾可夫模型（Hidden Markov Model, HMM）的研究中，Leonard E. Baum提出的基於MLE的HMM參數估計方法，即Baum-Welch算法（Baum-Welch algorithm）也是EM算法的特例之一。
理論
EM算法是基於極大似然估計（Maximum Likelihood Estimation, MLE）理論的最佳化算法。給定相互獨立的觀測數據
，和包含隱變數
、參數
的機率模型
，根據MLE理論， 的最優單點估計在模型的似然取極大值時給出：
。考慮隱變數，模型的似然有如下展開：
算法
標準算法
計算框架
EM標準算法是一組疊代計算，疊代分為兩部分，即E步和M步，其中E步“固定”前一次疊代的
，求解
使 取極大值；M步使用 求解
使 取極大值。EM算法在初始化模型參數後開始疊代，疊代中E步和M步交替進行。由於EM算法的收斂性僅能確保局部最優，而不是全局最優。因此通常對EM算法進行隨機初始化並多次運行，選擇對數似然最大的疊代輸出結果。以下給出EM算法E步和M步的推導。
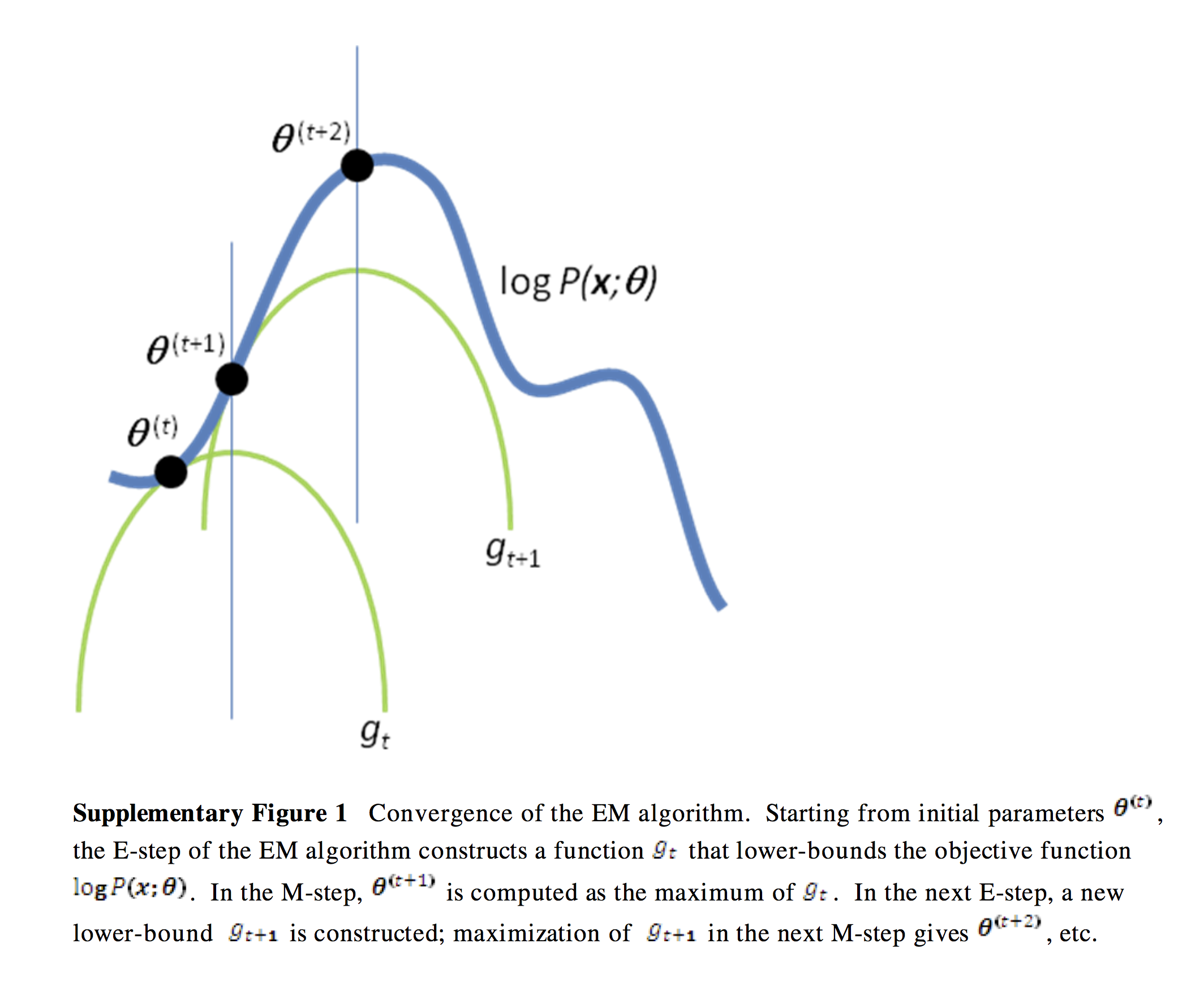
EM的計算框架：對數似然（藍），E步（綠），M步（實心點）
1. E步（Expectation-step, E-step）
由EM算法的求解目標可知，E步有如下最佳化問題：
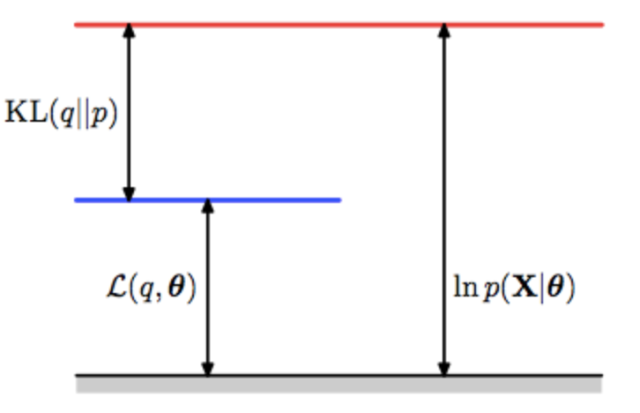
E步：最佳化代理損失（左），原最佳化目標（右）
2. M步（Maximization step, M-step）
在E步的基礎上，M步求解模型參數使 取極大值。該極值問題的必要條件是
：
計算步驟
將統計模型帶入EM算法的計算框架即可得到其計算步驟。這裡以高斯混合模型（Gaussian Mixture Model, GMM）為例進行說明。由GMM的一般定義可知，其似然和參數有如下表示：
將上述內容帶入EM算法的計算框架後，E步有如下展開：
M步通過E步輸出的隱變數後驗計算模型參數，在GMM中，M步計算框架的最佳化問題有如下表示：
根據以上計算步驟，這裡給出一個在Python 3環境使用EM算法求解GMM的編程實現：
# 導入模組
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import multivariate_normal
# 構建測試數據
N = 200; pi1 = np.array([0.6, 0.3, 0.1])
mu1 = np.array([[0,4], [-2,0], [3,-3]])
sigma1 = np.array([[[3,0],[0,0.5]], [[1,0],[0,2]], [[.5,0],[0,.5]]])
gen = [np.random.multivariate_normal(mu, sigma, int(pi*N)) for mu, sigma, pi in zip(mu1, sigma1, pi1)]
X = np.concatenate(gen)
# 初始化: mu, sigma, pi = 均值, 協方差矩陣, 混合係數
theta = {}; param = {}
theta['pi'] = [1/3, 1/3, 1/3] # 均勻初始化
theta['mu'] = np.random.random((3, 2)) # 隨機初始化
theta['sigma'] = np.array([np.eye(2)]*3) # 初始化為單位正定矩陣
param['k'] = len(pi1); param['N'] = X.shape[0]; param['dim'] = X.shape[1]
# 定義函式
def GMM_component(X, theta, c):
'''
由聯合常態分配計算GMM的單個成員
'''
return theta['pi'][c]*multivariate_normal(theta['mu'][c], theta['sigma'][c, ...]).pdf(X)
def E_step(theta, param):
'''
E步：更新隱變數機率分布q(Z)。
'''
q = np.zeros((param['k'], param['N']))
for i in range(param['k']):
q[i, :] = GMM_component(X, theta, i)
q /= q.sum(axis=0)
return q
def M_step(X, q, theta, param):
'''
M步：使用q(Z)更新GMM參數。
'''
pi_temp = q.sum(axis=1); pi_temp /= param['N'] # 計算pi
mu_temp = q.dot(X); mu_temp /= q.sum(axis=1)[:, None] # 計算mu
sigma_temp = np.zeros((param['k'], param['dim'], param['dim']))
for i in range(param['k']):
ys = X - mu_temp[i, :]
sigma_temp[i] = np.sum(q[i, :, None, None]*np.matmul(ys[..., None], ys[:, None, :]), axis=0)
sigma_temp /= np.sum(q, axis=1)[:, None, None] # 計算sigma
theta['pi'] = pi_temp; theta['mu'] = mu_temp; theta['sigma'] = sigma_temp
return theta
def likelihood(X, theta):
'''
計算GMM的對數似然。
'''
ll = 0
for i in range(param['k']):
ll += GMM_component(X, theta, i)
ll = np.log(ll).sum()
return ll
def EM_GMM(X, theta, param, eps=1e-5, max_iter=1000):
'''
高斯混合模型的EM算法求解
theta: GMM模型參數; param: 其它係數; eps: 計算精度; max_iter: 最大疊代次數
返回對數似然和參數theta，theta是包含pi、mu、sigma的Python字典
'''
ll_old = 0
for i in range(max_iter):
# E-step
q = E_step(theta, param)
# M-step
theta = M_step(X, q, theta, param)
ll_new = likelihood(X, theta)
if np.abs(ll_new - ll_old) < eps:
break;
else:
ll_old = ll_new
return ll_new, theta
# EM算法求解GMM，最大疊代次數為1e5
ll, theta2 = EM_GMM(X, theta, param, max_iter=10000)
# 由theta計算聯合常態分配的機率密度
L = 100; Xlim = [-6, 6]; Ylim = [-6, 6]
XGrid, YGrid = np.meshgrid(np.linspace(Xlim[0], Xlim[1], L), np.linspace(Ylim[0], Ylim[1], L))
Xout = np.vstack([XGrid.ravel(), YGrid.ravel()]).T
MVN = np.zeros(L*L)
for i in range(param['k']):
MVN += GMM_component(Xout, theta, i)
MVN = MVN.reshape((L, L))
# 繪製結果
plt.plot(X[:, 0], X[:, 1], 'x', c='gray', zorder=1)
plt.contour(XGrid, YGrid, MVN, 5, colors=('k',), linewidths=(2,))
改進算法
基於貝葉斯推斷（Bayesian inference）的EM算法
參見：變分貝葉斯EM
在MLE理論下，EM算法僅能給出模型參數 的單點估計，引入貝葉斯推斷方法後，EM算法能夠給出模型參數的後驗（posterior）分布避免過度擬合，其中常見的例子是極大後驗估計（Maximum A Posteriori estimation, MAP）的EM算法。MAP-EM在標準EM算法的基礎上引入了模型參數的先驗（prior）：
，此時MAP-EM的最佳化目標由模型的似然轉變為後驗，其離散形式可表示為：
MAP-EM在Dempster et al. (1977)就已被提出，但不同於標準EM，MAP-EM的隱分布是隱變數和模型參數的聯合分布，其對應的隱變數後驗
往往沒有解析形式。在貝葉斯體系下，求解該隱變數後驗的方法包括馬爾可夫鏈蒙特卡羅（Markov Chain Monte Carlo, MCMC）和變分貝葉斯估計（Variational Bayesian Inference, VBI），對前者，可證明由MCMC求解的MAP-EM等價於吉布斯採樣（Gibbs sampling）算法；對後者，由VBI求解的MAP-EM被稱為變分貝葉斯EM算法（Variational Bayesian EM algorithm, VBEM）。
VBEM使用平均場理論（Mean Field Theory, MFT）將隱分布近似為其在各個維度上分布的乘積：
並由此得到以下疊代步驟：
EM梯度算法（EM gradient algorithm）和廣義EM算法（Generalized EM algorithm, GEM）
參見：廣義期望最大算法
EM算法的M步通過計算偏導數求解代理函式的極大值，EM梯度算法（EM gradient algorithm）將該過程替換為牛頓疊代法（Newton-Raphson method）以加速疊代收斂。更進一步地，當代理函式 不是凸函式或無法有效地對 求解極大值時，可以使用廣義EM算法（GEM）。GEM有兩種實現方式，一是在M步使用非線性最佳化策略，例如共軛梯度算法（conjugate gradients algorithm），二是將原M步的求導計算分解為多個條件極值問題逐個計算模型參數，後者也被稱為最大條件期望算法（Expectation Conditional Maximization algorithm, ECM）。
EM算法的E步也可以按ECM的方法分解為條件極值問題，由先前推導可知，E步的最佳化問題僅有一個全局極大值，即隱分布 ，因此在E步將MLE的最佳化目標：聯合似然
對觀測樣本按因子展開並對每個展開分別使用EM算法，可以得到同樣的最佳化結果。對於M步，如果觀測樣本來自指數族分布，則M步也可以在每次疊代僅對有限個樣本的展開進行。在指數族問題中使用EM算法的上述推廣，可以避免在疊代中反覆處理整個觀測樣本集，降低計算開銷。
α-EM算法（α-EM algorithm）
α-EM算法是對標準算法的隱變數機率分布引入權重係數
的改進版本。標準的EM算法是α-EM算法在
時的特例。給定恰當的超參數 ，α-EM能夠比標準EM算法更快收斂。有研究將α-EM算法套用於神經網路的機率學習和隱馬爾可夫模型的參數估計。
性質
收斂性與穩定性：EM算法必然收斂於對數似然的局部極大值或鞍點（saddle point），其證明考慮如下不等關係：
計算複雜度：在E步具有解析形式時，EM算法是一個計算複雜度和存儲開銷都很低的算法，可以在很小的計算資源下完成計算。在E步不具有解析形式或使用MAP-EM時，EM算法需要結合其它數值方法，例如變分貝葉斯估計或MCMC對隱變數的後驗分布進行估計，此時的計算開銷取決於問題本身。
與其它算法的比較：相比於梯度算法，例如牛頓疊代法和隨機梯度下降（Stochastic Gradient Descent, SGD），EM算法的優勢是其求解框架可以加入求解目標的額外約束，例如在高斯混合模型的例子中，EM算法在求解協方差時可以確保每次疊代的結果都是正定矩陣。EM算法的不足在於其會陷入局部最優，在高維數據的問題中，局部最優和全局最優可能有很大差異。
