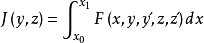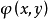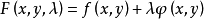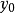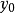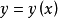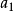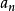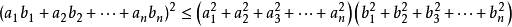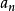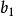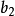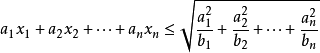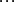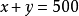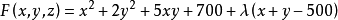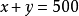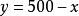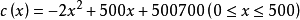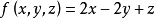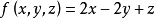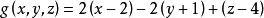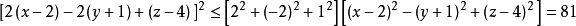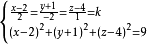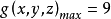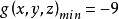條件極值

條件極值是在某附加條件下的極值。作為在數學中被廣泛套用的概念，無論是在數學中求解不等式，代數思想解決幾何問題，還是在經濟學中求效益最大化，工程項目的建設當中,對項目進度的管理 只要能在問題中抽象出此類模型模型。就能套用求條件極值的方法求解。

基本介紹

• 中文名：條件極值
• 外文名：conditional extremum/extremum with a condition/extremum with a constraint
• 別稱：約束極值
• 分類：數學
• 適用領域範圍：數學、物理、工程、經濟
• 特點：帶有一定附加條件

定義

通用定義

設函式f(x)與g₁(x)，…，g_m(x) (1≤m<n)在開集G⊂R上給定。記D為G中滿足限制條件g_j(x)=0，j=1，…，m的點x之集。設x₀∈D。若存在x₀的某個鄰域B(x₀，δ)，使得當x∈B(x₀，δ)，同時x∈D時有f(x)≤f(x₀)(f(x)≥f(x₀))，則稱x₀點為函式f在限制條件g_j(x)=0，j=1，…，m下的極大(小)值點。條件極大值點與條件極小值點統稱為條件極值點。條件極大值點與條件極小值點的函式值即為函式f(x)在限制條件g_j(x)下的條件極值。

數學辭海定義

泛函J在某附加條件下的極值.例如，泛函

函式y，z除滿足固定邊界條件

y(x₀)=y₀， y(x₁)=y₁， z(x₀)=z₀， z(x₁)=z₁

之外還滿足一個附加條件

或

這種問題的極值稱為條件極值.附加條件稱為約束.不含導數的約束，如G(x，y，z)=0，稱為有限約束或完整約束;含導數的約束，如G(x，y，z，y′，z′)=0，稱為微分約束或非完整約束.

求解

Lagrange

求二元函式在約束條件=0下的可能極值點.可以先作拉格朗日函式

其中 λ為拉格朗日乘子對

分別對拉格朗日函式每個變數求偏導並令其值為0，解出得到的駐點就是函式(l)在條件(2)下可能的極值點.至於所求得的點是否為極值點，需要在實際問題中根據問題本身的性質來判定.這也是解決條件極值的通用方法.

代入法

對於約束條件比較簡單的條件極值，還可以使用代入法將其化為無條件極值.即從前述條件(2)中解出或x一x伽)，然後將其代入函式(1)，原問題即可化為一元函式的極值問題.

柯西不等式法

柯西不等式是由大數學家柯西《}audry研究數學分析中的“流數，’問題時得到的一個非常重要的不等式，某些函式的極值、最值可以轉化為柯西不等式的形式求解柯西不等式:對於任意的實數,,,和,,,總有

簡述為‘‘積和方不大於方和積”;a; ER, b; ER，若且唯若實數,,,和,,,對應成比例時，等號成立[l }l由此，得到兩個重要結論:

(1)若 則

(2)若則 (其中,i=1,2n)

運用柯西不等式，主要是把目標函式適當變形，進而“配.湊n可西不等式的左邊或右邊的形式，最終求得極大值或極小值。

其他方法

均值不等式法、梯度法、圖像法、三角代換法，構造二次型等。最通用的還是拉格朗日乘數法，其他一些方法通常需要對應原函式的不同形式可以更方便的求解。

例題

例1

(成本最小問題)某公司的兩個工廠生產同樣的產品，但所需成本不同，第一個工廠生產x單位產品和第二個工廠生產Y單位產品時的總成本是

若公司的生產任務是500個單位產品，問如何分配任務才能使總成本為最小?

解法1

該問題是求函式在條件下的極值.作拉格朗日函式

分別對該拉格朗日函式的所有自變數x,y,λ求偏導，並令其值均為0，解得可能的極值點是(125,375).根據問題的實際性質，該點就是要求的最小值點.也就是說，當第一個工廠生產125單位產品、第二個工廠生產375單位
產品時總成本最小。

解法2

解法2由解出，並代入目標函式中，可得總成本

對總成本函式求導，並令其一階導數等於0，可得唯一駐點x=125，.由於。在該點的二階導數小於0，知該駐點是極大值點，所以也一定是最大值點.比較c(0),c(125),c (500)，可得所求最小值點x = 500.即第一個工廠生產500單位產品時總成本最小。

例2

已知求出的最值 解:首先將

變形為

再設

,

於是，根據柯西不等式(1)及已知條件，有

即

若且唯若

時，等號成立;

即當k=1;x=4;y=-3;z=5時;k=-1,x=0,y=1,z=3時

所以