龐特里亞金類有一些類似於斯蒂弗爾-惠特尼類與陳類的幾何與拓撲性質。此外，由於複數與四元數之間的密切關係，還存在一些陳類與龐類之間的關係，但是米爾諾(Milnor, J. W.)證明，龐特里亞金類不是拓撲不變數。
基本介紹
- 中文名：龐特里亞金類
- 外文名：Pontryagin class
- 適用範圍：數理科學
簡介,龐特里亞金數,
簡介
設ξ=（E,p,B,ℝn)是以仿緊的豪斯多夫空間B為低空間、ℝn為纖維、正交群O(n)為結構群的n維實向量叢。對應於結構群的包含映射O(n)➥U(n)，ξ與其復化叢
相對應。然後，ξ的龐特里亞金類可由其復化叢的陳類定義。
ξ的4i維龐特里亞金類指
和式
稱為ξ的全龐特里亞金類，記作p(ξ)。
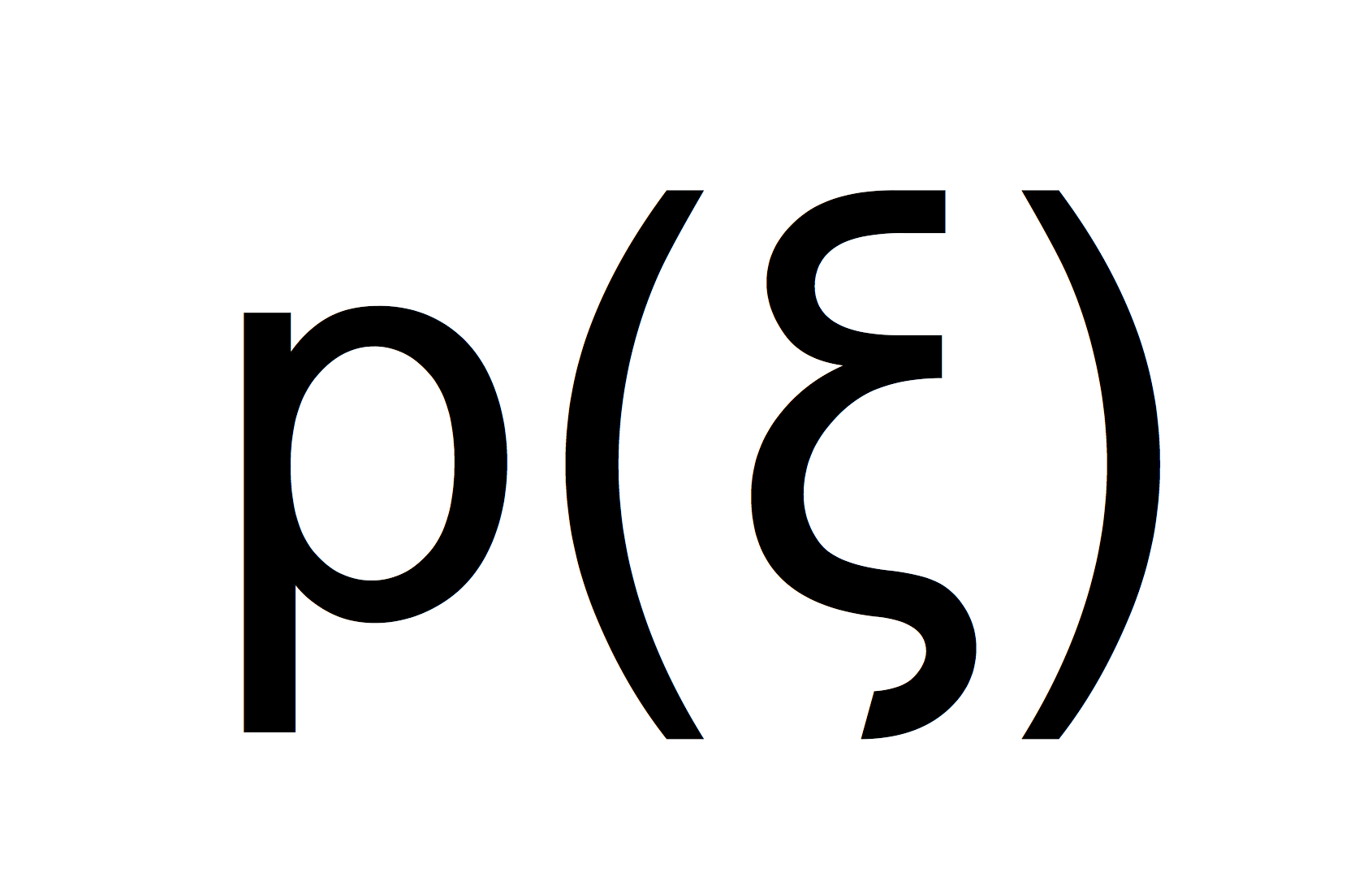
龐特里亞金類有一些類似於斯蒂弗爾-惠特尼類與陳類的幾何與拓撲性質。此外，由於複數與四元數之間的密切關係，還存在一些陳類與龐類之間的關係，但是米爾諾(Milnor, J. W.)證明，龐特里亞金類不是拓撲不變數。
龐特里亞金數
[Pontryagin number]
龐特里亞金數是微分流形的拓撲不變數，它是針對4n維流形而言，即若流形的維數不能被4整除，則其龐特里亞金數為零。設M是一個4n維微分流形。M的龐特里亞金數指它的龐特里亞金類生成的所有4n次單項式在基本同調類[M]的估值：
，其中
。
龐特里亞金數是定向配邊的不變數。龐特里亞金數和斯蒂弗爾-惠特尼數合在一起是可定向微分流形的定向配邊類的完全不變數。整性定理中的一些重要不變數（諸如希策布魯赫符號差，Â虧格等）均可由龐特里亞金數表達。
