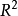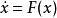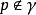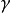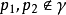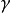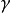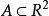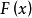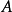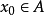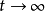龐加萊-本迪克松定理(Poincaré-Bendixson theorem)是平面定性理論的經典成果並是後續研究的重要基礎。給定系統dx/dt=X(x),(1),或平面系統:dx/dt=P(x,y),dy/dt=Q(x,y),(2),龐加萊-本迪克松定理斷言:若系統(2)的一條正半軌保持在某一不含奇點的有界區域內,則它盤旋逼近於一條極限環(它在該軌線所在一側為穩定)。設有集合A,如果對任一x∈A及一切t∈R,(1)或(2)的軌線φt(x)∈A,則稱A為系統(1)或(2)的不變集。顯然,ω或α極限集均為不變集。如果不存在A的不變真子集,則非空不變集A稱為一個極小集。關於極小集的結構,施瓦茲(A.J.Schwarz)於1963年將上述結果推廣到定義於二維流形上的C2類流,得到下述結論(亦稱施瓦茲定理):C2類流形M上的C2流的非空緊極小集必屬於下列情形之一:1.一個奇點;2.一條閉軌;3.整個流形M。對維數n>2的系統,則可以有結構複雜的極限集,例如混沌集等。
基本介紹
- 中文名:龐加萊-本迪克松定理
- 外文名:Poincaré-Bendixson theorem
- 所屬學科:數學
- 所屬問題:常微分方程定性理論
- 相關概念:定性理論、不變集等
基本介紹
定理

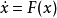



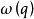
注意點
證明思路
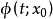

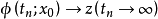


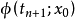


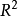
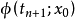



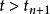
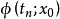
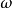
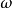
 圖1
圖1推論