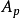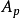基本介紹
- 中文名:極小集
- 外文名:minimal set
- 所屬學科:數學(動力系統)
- 屬性:動力系統一個重要的不變集合
基本介紹,相關性質,極小集的存在性,
基本介紹
換句話說,如果 在極小集M內有一個緊緻的不變集
在極小集M內有一個緊緻的不變集 ,那么K= M。由此可以導出許多有趣的性質例如,設M 是
,那么K= M。由此可以導出許多有趣的性質例如,設M 是 的極小集,則
的極小集,則 。從而
。從而 。因此,
。因此, 也是緊緻的。由
也是緊緻的。由






極小集的定義,就推出


相關性質
定理1 設軌線 是正向(或負向)B-式回復的,則它的閉包
是正向(或負向)B-式回復的,則它的閉包 是一個極小集。
是一個極小集。


定理2設M是動力系統 的極小集,則過任一點
的極小集,則過任一點 的運動
的運動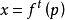 是(雙向)B-式回復的。
是(雙向)B-式回復的。


定理2說明,在極小集中的運動都是(雙向) B-式回復的。因此,極小集是鑑別B-式回復運動的一個簡單的幾何方法。
注意,極小集一定是準極小集,而且它的每條軌線(在極小集內) 都是處處稠密和雙向B-式回復的。然而,在準極小集內不一定每條軌線都是處處稠密的。
極小集的存在性
下述命題是著名的極小集存在定理。
定理3設 是動力系統
是動力系統 的(非空)緊緻不變集,則
的(非空)緊緻不變集,則 在K內至少有一個極小集。
在K內至少有一個極小集。



這裡順便指出,動力系統 的
的 極限點集
極限點集 和
和 極限點集
極限點集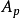 都是不變的閉集。因此,當
都是不變的閉集。因此,當 或
或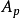 是緊緻時,
是緊緻時, 的極小集是存在的,從而
的極小集是存在的,從而 的B-式回復運動也是存在的,它們可以是平凡的,也可以是非平凡的。特別,對於平面動力系統,極小集都是平凡的(它們不是奇點就是閉軌)。這樣,由極小集存在定理可以得到下述Poincaré-Bendixson定理:
的B-式回復運動也是存在的,它們可以是平凡的,也可以是非平凡的。特別,對於平面動力系統,極小集都是平凡的(它們不是奇點就是閉軌)。這樣,由極小集存在定理可以得到下述Poincaré-Bendixson定理:




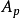

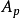


如果平面動力系統 有一個正向(或負向)有界的運動
有一個正向(或負向)有界的運動 ,而且它的正向極限點集
,而且它的正向極限點集 (或負向極限點集
(或負向極限點集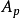 )不包含奇點,則
)不包含奇點,則 (或
(或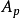 )是一條閉軌。
)是一條閉軌。