齊次泊松過程(homogeneous Poisson process )是一類既簡單又在理論和套用中起著重要作用的隨機點過程。
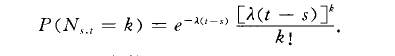
齊次泊松過程(homogeneous Poisson process )是一類既簡單又在理論和套用中起著重要作用的隨機點過程。
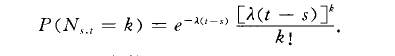
齊次泊松過程(homogeneous Poisson process )是一類既簡單又在理論和套用中起著重要作用的隨機點過程。...
一種累計隨機事件發生次數的最基本的獨立增量過程。例如隨著時間增長累計某電話交換台收到的呼喚次數,就構成一個泊松過程。 泊松過程是由法國著名數學家泊松(Poisson,...
廣義齊次泊松過程(generalized homogeneousPoisson process)亦稱平穩無後效流一種齊次泊松過程.在齊次泊松過程的定義中除去有序性條件就得到廣義齊次泊松過程。可以證明,...
重隨機泊松過程(doubly stochastic Poissonprocess)亦稱柯克斯過程一類隨機點過程。是柯克斯於1955年在研究處於隨機環境的泊松過程時引入的。這類過程可以看做是點發生...
自激點過程(self-exciting point process)是一類強度可以依賴於過程自身歷史的點過程.齊次泊松過程的強度是一常數,如果允許強度隨時間t改變就得到帶時倚強度的泊松...
3.4 非齊次泊松過程 3.5 複合泊松過程 3.6 過濾的泊松過程 3.6.1 電子系統中的過濾泊松過程 3.6.2 過濾泊松過程的統計特性 3.6.3 條件泊松過程的概念 3.7 維...
齊次泊松過程和平衡更新過程都是平穩點過程的特例 [1] 。中文名 平穩點過程 外文名 stationary point process 所屬學科 數學 所屬問題 隨機過程(隨機點過程與...
(2)在任意時間間隔s內,失效數量服從均值為 的泊松分布,也就是說(3)初始條件為N(0)=0。這一模型也叫做齊次泊松過程,這也暗示了故障率 不由時間t決定。也就...
2??2齊次泊松過程的定義 2??3齊次泊松過程的點發生時間和計數的條件分布 2??4廣義齊次泊松過程 2??5帶時倚強度的泊松過程 2??6非齊次泊松過程 2??7一般泊...
3.1 泊松過程的定義和數字特徵 3.2 與泊松過程相關的分布 3.3 泊松過程的檢驗及參數估計 3.4 非齊次泊松過程 3.5 複合泊松過程 3.6 更新過程 習題4...
獨立增量過程,狀態離散的平穩獨立增量過程是一類特殊的馬爾可夫過程。泊松過程和布朗運動都是它的特例。從一般的獨立增量過程分離出本質上是獨立隨機變數序列的部分和...
圖書內容本書主要討論隨機過程的基礎理論和套用方法。全書共七章,內容包括:機率論基礎,隨機過程基礎,泊松過程及其推廣,馬爾可夫過程,二階矩過程及其均方分析,平穩過程...
NHPP,Non-homogeneous Poisson process,中文名非齊次泊松過程模型,屬於指數類失效時間模型...
1) 敖長林、李一軍,基於非齊次泊松過程的發動機使用可靠性,機械工程學報,2007,43(10)206-210 (EI收錄)2) 敖長林,李一軍,馮磊,焦揚,基於CVM的三江平原濕地非使用...
更新定理(renewal theorem)一類有關更新過程的極限定理。常見的有初等更新定理、布萊克韋爾關鍵更新定理、史密斯關鍵更新定理等。更新理論是將泊松過程概括為任意持有時間...
B.2HPP(齊次泊松過程)的驗證試驗 B.3威布爾分布的測定試驗 B.4冪律模型的測定試驗(例1) B.5恆定失效強度的比較試驗 B.6成功/失敗率的驗證試驗 B...
5.4 泊松過程的生成5.5 非齊次泊松過程的產生習題參考文獻第6章 離散事件模擬法6.1 離散事件模擬法6.2 單服務員排隊系統6.3 兩個服務員的串聯排隊系統...
二、齊次泊松過程的模擬 三、馬爾可夫鏈的模擬 12.6 定積分的機率計算方法 一、常用的兩種算法 二、重積分的計算 12.7 某些方程的機率解法 一、線性方程組的...
