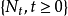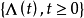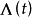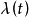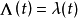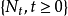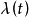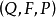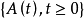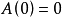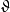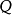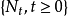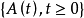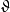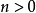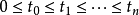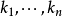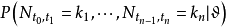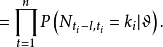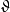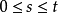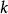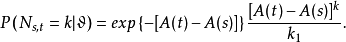概述
重隨機泊松過程(doubly stochastic Poissonprocess)亦稱柯克斯過程一類隨機點過程。是柯克斯於1955年在研究處於隨機環境的泊松過程時引入的。這類過程可以看做是點發生強度本身是一個隨機過程(稱為強度過程)的泊松過程。其中強度過程是由反映周圍環境或被傳送的信息等外部因素支配的。更確切地說,重隨機泊松過程在給定了強度過程的條件下是具有給定強度的泊松過程。因此這類過程也稱為條件泊松過程。
定義和例子
通過允許泊松過程的強度不僅可隨時間而變化,而且還會隨環境等因素隨機地改變,即強度本身是一非負實值隨機過程時,我們就得到所謂重隨機泊松過程。
定義1:點過程
稱做具有強度過程
的重隨機泊松過程(doubly stochastic Poissonprocess),如果對於過程
的幾乎所有現實
,當給定
時點過程
是具有時倚強度
的泊松過程。
因為按定義,重隨機泊松過程是在給定了隨機強度的條件下是一(帶時倚強度的)泊松過程,所以人們又把這類過程稱作條件泊松過程。
D.Cox於1955年首先引入並討論了重隨機泊松過程,所以也有人把這類過程稱作Cox(柯克斯)過程。他在研究由於緯紗中斷引起紡紗機的停機問題時認為,如果紡紗機的工作環境(如溫度、濕度等)和使用的緯紗質量完全不變時,緯紗中斷的現象可用一具有常數強度
的齊次泊松過程來描述。但是,實際上由於工作環境會發生變化,緯紗的質量(例如,來源不同)也可能變化,因而強度
也隨之改變。所以不能簡單地用一強度恆定不變的
齊次泊松過程描述緯紗中斷現象。由於工作環境和緯紗質量的變化通常是隨機的,從而強度的改變也是隨機的。為了描述這樣的緯紗中斷引起的停機事件,我們必須引入和研究重隨機泊松過程。
在物理學中也有類似的現象。例如,雷射通訊系統的傳送部分發出作為載波的雷射投射到接收部分的光檢測器上。雷射引起的光電子流形成一泊松過程,要傳輸的信號被轉化為一定頻率和相位的無線電波(稱作副載波)後用來調製載波的雷射強度。這樣,在接收部分的檢測器接收到的光電子流形成一強度隨機變化的泊松過程,即重隨機泊松過程。
定義2:設
是基本機率空間,
是一滿足
(以機率1)的非負不減右連續實值隨機過程。以
表示在
上使得過程
可測的最小
代數。我們把點過程
稱作具有累積強度過程(又稱均值過程)
的重隨機泊松過程,如果它滿足下列兩條件:
1、對
有條件獨立增量,即對任意整數
,實數
和非負整數
,以機率1有
2、對
有條件泊松分布,即對任意
和非負整數
,以機率1有