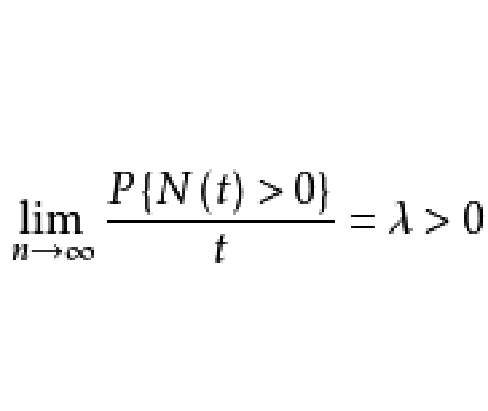平穩點過程

平穩點過程(stationary point process)是一種隨機點過程，在許多文獻中是指具有平穩增量的隨機點過程(等價地說，計數過程){N(t)，t≥0}，即對任意實數t>s≥0和h>0，過程在區間(s，t]和(s+h，t+h]中的點數(或者說，增量N_s，t=N(t)-N(s)和N_s+h，t+h=N(t+h)-N(s+h))有相同的分布。齊次泊松過程和平衡更新過程都是平穩點過程的特例。

基本介紹

• 中文名：平穩點過程
• 外文名：stationary point process
• 所屬學科：數學
• 所屬問題：隨機過程(隨機點過程與分支過程)
• 相關概念：隨機點過程

基本介紹

具有平穩增量的計數過程稱為平穩點過程。平衡更新過程是平穩點過程的一個例子。

應當指出，有些文獻把這一術語用於對任意有限多個區間，其增量有平穩聯合分布的點過程。即對任意整數和實數和，增量

和

有相同的k維聯合分布。這時，為了把前面提到的具有平穩區間分布的點過程和這種具有較強的平穩性要求的點過程區別開來，常常把前者稱為粗平穩點過程。

相關定理及證明

定理1 除了對一切有的平凡情形以外，對任意平穩點過程有

其中並不排除。

證明： 令且注意到取非負值，且非減，又

因此

而由歸納法，對一切有

於是，令a使，對一切有

現在定義，由(2)我們得

為了證明，我們考慮兩種情形。首先，假設，此時，固定，取使。現在對存在一個整數n使

由的單調性和式(2)可知，對這個區間中的一切t有

因此

由於是任意的，且當時，由此推出。

現在假定，此時，固定任意很大的A>0，取s使，則由式(3)推出對一切有

它蘊含，這就完成了證明。