隨機點過程是描述按一定統計規律在空間X中隨機地分布的一些點的數學模型。
基本介紹
- 中文名:隨機點過程
- 外文名:stochastic point process or ran-dom point process
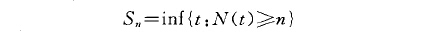
隨機點過程是描述按一定統計規律在空間X中隨機地分布的一些點的數學模型。
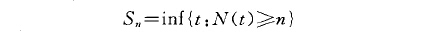
隨機點過程是描述按一定統計規律在空間X中隨機地分布的一些點的數學模型。隨機點過程(stochastic point process or ran-dom point process)簡稱點過程。一類數學模型。它是描述按一...
描述隨機點分布的隨機過程。很多隨機現象發生的時刻、地點、狀態等往往可以用某一空間上的點來表示。例如,服務台前顧客的到來時刻,真空管陰極電子的發射時刻,可表為實軸上的點。又如,天空中某一區域內星體的分布,核醫療中放射性示蹤...
齊次泊松過程(homogeneous Poisson process )是一類既簡單又在理論和套用中起著重要作用的隨機點過程。可以這樣說,隨機點過程是以這類過程為基石發展起來的.對於計數過程{N(t),t>0},如果它滿足以下條件:1 .P(N(0)=0)=1;2.有...
《隨機點過程及其套用》是1998年由科學出版社出版的圖書,該書作者是鄧永錄。內容介紹 本書共分11章,前9章較全面和詳細地介紹一些常用的點過程模型及其套用.通過這些內容的學習使讀者對點過程的模型、物理背景、方法、理論和可能的套用...
《運用隨機點過程對限價指令簿進行隨機建模及研究》是依託深圳大學,由董海玲擔任項目負責人的青年科學基金項目。項目摘要 本項目以指令驅動市場(如滬、深兩市)的限價指令簿為研究對象,以克服現有隨機模型的局限和不足為切入點,探索構建...
重隨機泊松過程(doubly stochastic Poissonprocess)亦稱柯克斯過程一類隨機點過程。是柯克斯於1955年在研究處於隨機環境的泊松過程時引入的。這類過程可以看做是點發生強度本身是一個隨機過程(稱為強度過程)的泊松過程。其中強度過程是由...
《Markov過程、隨機點過程與風險理論》是依託南開大學,由郭軍義擔任項目負責人的面上項目。中文摘要 本項目研究幾類隨機過程包括馬氏過程、COX過程、多元相依過程等的理論及在風險理論中的套用。深入研究馬程首中和末離分布並找出與破產機率...
多維點過程 多維點過程(multidimensional point process)一類隨機點過程。指點發生空間是多維空間的隨機點過程.
若對{(Tₙ,Yₙ),n≥1}的統計特性不作任何假定,這樣規定的X 便是一種一般地描述系統跳躍變化的隨機過程,常稱為標值點過程,也稱多變點過程或跳躍過程。泊松過程除作為計數過程的一種重要數學模型外,又是眾多重要隨機過程的...
《行列式點過程的機率分析》是依託浙江大學,由蘇中根擔任項目負責人的面上項目。項目摘要 行列式點過程是一類具有良好代數結構的特殊隨機點過程,其相關函式可以用核函式的行列式表示。它廣泛地出現在隨機矩陣、隨機劃分、隨機增長模型、隨機...
隨機過程 在當代科學與社會的廣闊天地里,人們都可以看到一種叫作隨機過程的數學模型:從銀河亮度的起伏到星系空間的物質分布、從分子的布朗運動到原子的蛻變過程,從化學反應動力學到電話通訊理論、從謠言的傳播到傳染病的流行、從市場預測...
跳過程(jump process)指的是跳躍地取值的隨機過程。設給定基本機率空間(12, ,P)及上升,域族(F __t) , (X>.)。是取值於相空間(E,.)的隨機過 程.它稱為跳過程,如果它分段為常值且在任意有限 區間只有有限個跳躍點,...
表示時刻 n 質點的位置,則過程 稱為隨機遊動,由假設 表示質點的第 k 次位移,由假設 { } 獨立分布:而對 ,有 於是它是平穩獨立增量過程,從而是離散時間時齊馬爾可夫鏈,其一步轉移機率為 若質點可以在整個數軸的整數點上遊動...
馬爾可夫過程(Markov process)是一類隨機過程。它的原始模型馬爾可夫鏈,由俄國數學家A.A.馬爾可夫於1907年提出。馬爾可夫過程是研究離散事件動態系統狀態空間的重要方法,它的數學基礎是隨機過程理論。概念 1.馬爾可夫性:設 為一隨機...
《複雜空間點過程數據的統計推斷》是依託昆明理工大學,由吳劉倉擔任項目負責人的數學天元基金項目。項目摘要 在許多學科研究領域(如:地質生態學、生物醫學、經濟學)中經常需處理從不同空間位置、不同時間蒐集來的空間時間隨機點過程複雜...
《隨機過程、隨機分形理論及其相關套用》是依託中國科學院大學,由胡曉予擔任項目負責人的面上項目。項目摘要 擬研究隨機過程和隨機場的幾何性質,研究隨機環境中的隨機過程,探索分形理論和隨機過程在生物和醫學等學科中的套用。.關於傳統...
