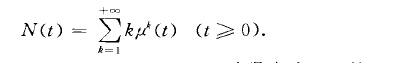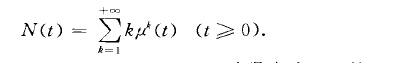廣義齊次泊松過程(generalized homogeneousPoisson process)亦稱平穩無後效流一種齊次泊松過程.在齊次泊松過程的定義中除去有序性條件就得到廣義齊次泊松過程。可以證明,若{N(t),t妻0}是廣義齊次泊松過程,則對任意t}O,N(t)的機率母函式
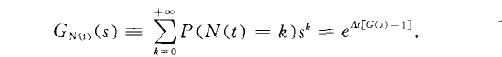
其中人》o是一常數,G(s)是某一正整值隨機變數的機率
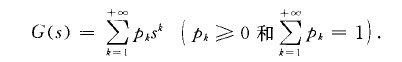
因為上面的}N(r> (S)可由在齊次泊過程的機率母函式。NC‘一‘」中用G (s)替換、而得,故可以構想廣義齊次泊松過程是經由以下兩步產生:首先,以給定的a作強度確定一齊次泊松過程{M(t) ,t妻0};然後由這過程確定廣義泊松過程{N(t),t>0}的點(亦即跳躍)發生時刻.在每一個這樣的時刻有k個點(即躍度為k的跳躍)的機率是pk(k=1,2,3,...),而且各個時刻發生的點數是相互獨立的。廣義齊次泊松過程有如下的分解表示:N(:)一藝k }k(‘)(‘)0).
其中切k(t),t乒。}(k=1>2}3,w)是強度為ap*的相互獨立的齊次泊松過程(參見“齊次泊松過程”).