基本介紹
介紹
算法


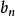
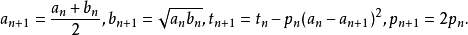
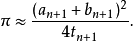
數學背景
算術-幾何平均數的極限
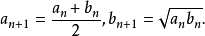
若 a0=1且
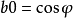
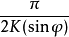
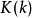
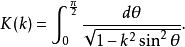
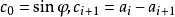
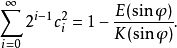
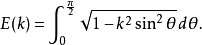
勒讓德恆等式

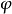
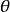
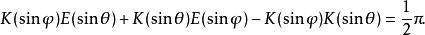
高斯-歐拉法
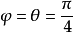
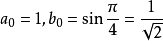
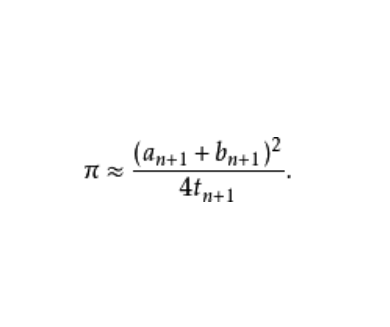


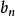
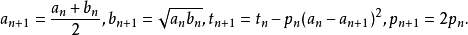
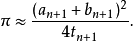
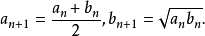
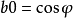
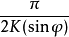
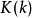
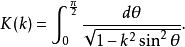
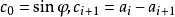
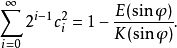
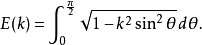

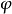
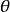
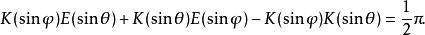
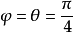
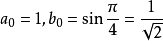
高斯-勒讓德算法是一種用於計算π的算法。它以迅速收斂著稱,只需25次疊代即可產生π的4500萬位正確數字。不過,它的缺點是記憶體密集,因此有時它不如梅欽類公式使用...
高斯一勒讓德求積公式(Gauss-Legendre qua-drature)是一種高斯型求積公式,用來解決函式問題。...
阿德利昂·瑪利·埃·勒讓德(公元1752年9月18日- 1833年1月10日)為法國數學家,生於巴黎,卒於同地。約1770年畢業於馬扎蘭學院。1775年任巴黎軍事學院數學教授...
高斯-勒讓德公式:(見圖)這個公式每疊代一次將得到雙倍的十進制精度,比如要計算100萬位,疊代20次就夠了。1999年9月,日本的高橋大介和金田康正用這個算法計算到...
這算法被稱為布倫特-薩拉明(或薩拉明-布倫特)演算法,亦稱高斯-勒讓德演算法。1989年美國哥倫比亞大學研究人員用克雷-2型(Cray-2)和IBM-3090/VF型巨型電子計算機...
4.6.2 高斯-勒讓德求積公式(121) 4.6.3 高斯-切比雪夫求積公式(123) 4.6.4 無窮區間的高斯型求積公式(124) 4.7 多重積分(126) 4.8 數值微分(128) 4.8.1...
Super PI是一個計算圓周率的電腦程式,最大精確到小數點以後的3200萬位數。該程式採用高斯-勒讓德算法,並且於1995年被日本計算機科學家金田康正使用在Windows環境下...
8.5.3高斯 勒讓德求積公式8.5.4高斯 切比雪夫求積公式8.6數值微分8.6.1差商公式及誤差分析8.6.2插值型求導公式8.6.3三次樣條求導習題8...
6.4.1變步長求積公式167 6.4.2龍貝格算法169 6.4.3理查森外推算法172 6.5高斯求積公式173 6.5.1高斯型求積公式的概念與性質173 6.5.2高斯—勒讓德求積公式...
5.5.2牛頓 科茨求積公式5.6高斯積分法5.6.1高斯積分法的基本思想5.6.2勒讓德 高斯求積公式5.6.3埃爾米特 高斯求積公式5.6.4拉蓋爾 高斯求積公式5.7龍貝格積分法...
4.5.3勒讓德多項式 4.5.4高斯求積公式的餘項 4.5.5高斯求積公式的穩定性與收斂性 4.6數值積分的神經網路算法 4.6.1餘弦基函式神經網路模型 4.6.2數值積...
5.8.4 高斯一勒讓德求積公式的MA'TLAB實現及套用實例5.9 數值微分第6章 常微分方程初值問題數值解法6.1 求解常微分方程的MATLAB符號法...
容易看到,高斯和勒讓德提出的漸進公式是等階的,實際上都等同於猜想π(x)~(不過高斯更深刻和精確)。這就是19世紀最著名的數學難題——素數定理。這個猜想是非常...
18.3.2兩點高斯-勒讓德公式的推導 45318.3.3更多點的公式 45618.4自適應求積 45718.5案例研究:均方根電流 45918.6習題 462...
阿基米德用到了疊代算法和兩側數值逼近的概念,稱得上是“計算數學”的鼻祖。 中國古算書《周髀算經》(約公元前2世紀)的中有“徑一而周三”的記載,意即取 。[5...
4.6.2 高斯-勒讓德求積公式(121)4.6.3 高斯-切比雪夫求積公式(123)4.6.4 無窮區間的高斯型求積公式(124)4.7 多重積分(126)4.8 數值微分(128)...
5.5.2牛頓 科茨求積公式5.6高斯積分法5.6.1高斯積分法的基本思想5.6.2勒讓德 高斯求積公式5.6.3埃爾米特 高斯求積公式5.6.4拉蓋爾 高斯求積公式5.7龍貝格積分法...
5.3 遞歸公式與龍貝格積分5.4 高斯-勒讓德積分(選讀)Chapter6 微分方程求解6.1 微分方程導論6.2 歐拉方法6.3 休恩方法AppendixAMATLAB簡介...
伽瑪函式Stirling公式 編輯 Gamma 函式從它誕生開始就被許多數學家進行研究,包括高斯、勒讓德、魏爾斯特拉斯、劉維爾等等。這個函式在現代數學分析中被深入研究,在...
