高斯濾波是一種線性平滑濾波,適用於消除高斯噪聲,廣泛套用於圖像處理的減噪過程。通俗的講,高斯濾波就是對整幅圖像進行加權平均的過程,每一個像素點的值,都由其本身和鄰域內的其他像素值經過加權平均後得到。高斯濾波的具體操作是:用一個模板(或稱卷積、掩模)掃描圖像中的每一個像素,用模板確定的鄰域內像素的加權平均灰度值去替代模板中心像素點的值。
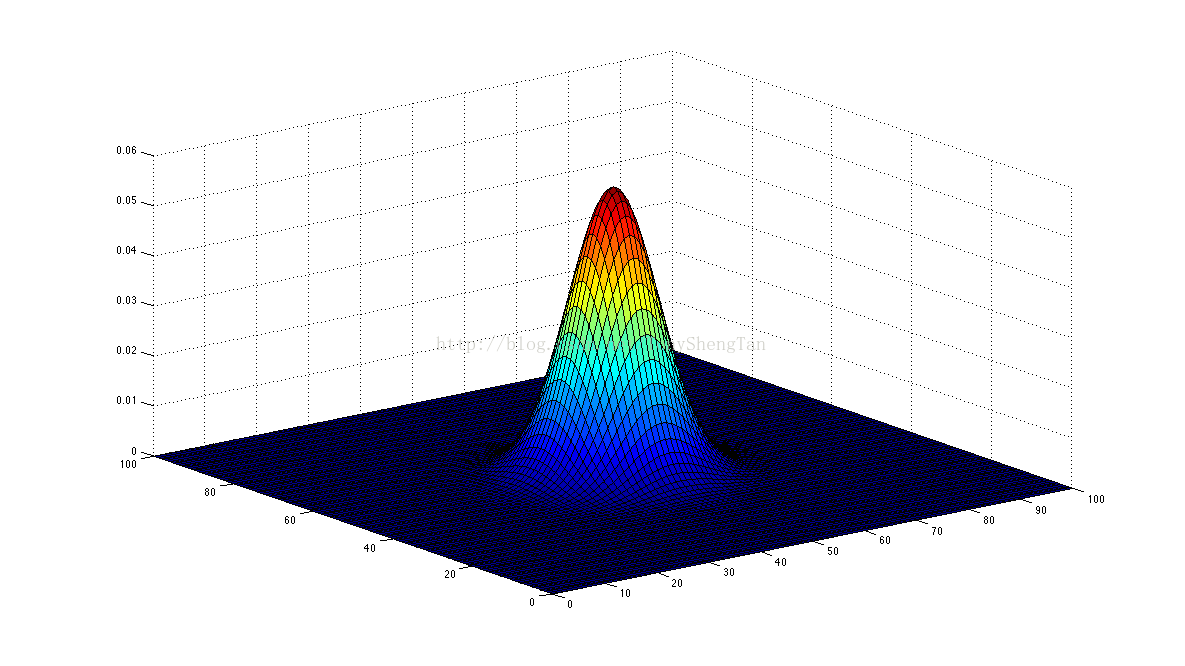
高斯濾波
相關詞條
- 高斯濾波
高斯濾波是一種線性平滑濾波,適用於消除高斯噪聲,廣泛套用於圖像處理的減噪過程。通俗的講,高斯濾波就是對整幅圖像進行加權平均的過程,每一個像素點的值,都由其...
- 高斯濾波最小頻移鍵控
這是GSM系統採用的調製方式。數字調製解調技術是數字峰窩移動通信系統空中接口的重要組成部分。GMSK調製是在MSK(最小頻移鍵控)調製器之前插入高斯低通預調製濾波器...
- 高斯濾波器
高斯濾波器是一個低通濾波器...... ,可以證明,高斯濾波器可用均值濾波器多次逼近,一般情況下,大於或等於三次逼近就可近似於高斯濾波器,所以,在設計高斯濾波器時,...
- 高斯模糊
高斯模糊(英語:Gaussian Blur),也叫高斯平滑,是在Adobe Photoshop、GIMP以及Paint.NET等圖像處理軟體中廣泛使用的處理效果,通常用它來減少圖像噪聲以及降低細節層次。...
- 平滑濾波
平滑濾波是低頻增強的空間域濾波技術。它的目的有兩類:一類是模糊;另一類是消除噪音。空間域的平滑濾波一般採用簡單平均法進行,就是求鄰近像元點的平均亮度值。...
- 高斯核函式
(2)高斯函式是單值函式.這表明,高斯濾波器用像素鄰域的加權均值來代替該點的像素值,而每一鄰域像素點權值是隨該點與中心點的距離單調增減的.這一性質是很重要...
- 中值濾波器
中值濾波是一種非線性數字濾波器技術,經常用於去除圖像或者其它信號中的噪聲。這個設計思想就是檢查輸入信號中的採樣並判斷它是否代表了信號,使用奇數個採樣組成的...
- 頻域平滑濾波
圖像的平滑除了在空間域中進行外,也可以在頻率域中進行。由於噪聲主要集中在高頻部分,為去除噪聲改善圖像質量,濾波器採用,然後再進行逆傅立葉變換獲得濾波圖像,就可...
- 高斯頻移鍵控
高斯頻移鍵控GFSK - Gauss frequency Shift Keying ,是在調製之前通過一個高斯低通濾波器來限制信號的頻譜寬度。...
- 跟蹤濾波工程——高斯-牛頓及多項式濾波
《跟蹤濾波工程——高斯-牛頓及多項式濾波》是2015年3月國防工業出版社出版的圖書,作者是(南非)諾曼·莫里森(Norman Morrison)。...
- 雙邊濾波
雙邊濾波(Bilateral filter)是一種非線性的濾波方法,是結合圖像的空間鄰近度和像素值相似度的一種折中處理,同時考慮空域信息和灰度相似性,達到保邊去噪的目的。...
- 高斯最小頻移鍵控
高斯最小頻移鍵控是基帶數位訊號經高斯低通濾波器處理的MSK調製。為了減少已調信號的頻譜寬度,可以減少高斯低通濾波器的歸一化頻寬BTb(Tb是比特寬度),BTb常取0.2...
- log(高斯拉普拉斯函式)
LoG邊緣檢測運算元是David Courtnay Marr和Ellen Hildreth(1980)共同提出的。因此,也稱為邊緣檢測算法或Marr & Hildreth運算元。該算法首先對圖像做高斯濾波,然後再求其...
- GMSK
高斯最小頻移鍵控(Gaussian Filtered Minimum Shift Keying),這是GSM系統採用的調製方式。數字調製解調技術是數字蜂窩移動通信系統空中接口的重要組成部分。GMSK調製是...
