“統計初步”這部分內容中,平均數是一個非常重要而又有廣泛用途的概念,在日常生活中,我們經常會聽到這樣一些名詞:平均氣溫、平均降雨量、平均產量、人均年收入等;而平均分數、平均年齡、平均身高等名詞更熟悉。
基本介紹
- 中文名:加權平均
- 外文名:The weighted average
- 學科:統計學
- 解釋:反映了一組數據的一般水平
統計學名詞
加權公式



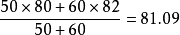

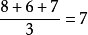



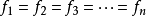

介紹



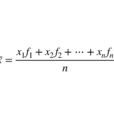
“統計初步”這部分內容中,平均數是一個非常重要而又有廣泛用途的概念,在日常生活中,我們經常會聽到這樣一些名詞:平均氣溫、平均降雨量、平均產量、人均年收入等;而平均分數、平均年齡、平均身高等名詞更熟悉。



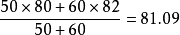

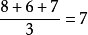



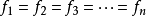




“統計初步”這部分內容中,平均數是一個非常重要而又有廣泛用途的概念,在日常生活中,我們經常會聽到這樣一些名詞:平均氣溫、平均降雨量、平均產量、人均年收入等;而...
加權平均法,利用過去若干個按照時間順序排列起來的同一變數的觀測值並以時間順序數為權數,計算出觀測值的加權算術平均數,以這一數字作為預測未來期間該變數預測值的...
加權平均值即將各數值乘以相應的權數,然後加總求和得到總體值,再除以總的單位數。加權平均值的大小不僅取決於總體中各單位的數值(變數值)的大小,而且取決於各數值...
儘管完全棘輪條款曾經很流行,現在也常常出現在投資人的Term Sheet里,但最常見的防稀釋條款還是基於加權平均的。加權平均條款,即如果後續發行的股份價格低於前一輪的...
加權平均成績是指每門成績乘以它的權值比例後算出的平均成績,算法為每門成績乘以它的權值比例。加權平均成績的計算比較類似GPA的算法。含義舉例不同的科目,所占的...
加權平均利率是指通過有關計算公式得出的能夠大體反映混合貸款成本的利率。 為構建固定資產借入一筆以上的一般借款,則資本化率應為這些一般借款的加權平均利率。...
加權幾何平均數是在變數值次數(或比重)不相等時,用加權的方法計算出的幾何平均數。幾何平均數是n個正標誌值的連乘積的n次方根。當標誌值出現的次數相同時,用...
加權平均價是指用數量作為權數進行平均計算的價格。...... 例如,石油輸出國組織官方出售的原油加權平均價,就是按石油輸出國組織13個成員國政府直接出售的原油的價格...
加權平均法是指標綜合的基本方法,具有兩種形式,分別為加法規則與乘法規則。加權平均法又稱“綜合加權平均法”、“全月一次加權平均法”。存貨成本,計算出存貨的加權...
加權平均數指數(weighted average index number)是計算總指數的另一種形式。它是以某一時期的總量為權數對個體指數加權平均計算出來的。其基本特點是:先計算出各個...
全月一次加權平均法。以數量為權數計算每種材料的實際平均單價,作為日常發料憑證的計價依據。全月一次加權平均法是指在月末計算一次平均單價,用該單價乘以發出材料...
所謂加權平均成本WACC(Weighted Average Cost of Capital)是指以某種籌資方式所籌措的資本占資本總額的比重為權重,對各種籌資方式獲得的個別資本的成本進行加權平均所...
每科成績乘以加權值,零點幾之類,最後再把成績相加就可以了。舉個例子,大學裡面都是學分制的,要求加權成績,就是把每科成績乘以學分,然後加起來,最後除以學分之...
移動加權平均法指企業按實際成本進行材料明細分類核算時,以各批材料收入數量和上批結餘材料數量為權數,計算材料平均單位成本的一種方法。採用這種計價方法,每購進一批...
時間加權平均值是美國政府工業衛生專家協會(ACGIH)制訂的閾限表中所規定的一種限量濃度。...
加權平均價格,運用加權算術平均法計算出的價格。通常用於蔬菜價格的評價。因蔬菜季節性強、品種多、價格波動大。採用加權價,菜代金能做到較公平合理,相對穩定,便於...
有算術平均值,幾何平均值,平方平均值(均方根平均值,rms),調和平均值,加權平均值等其中以算術平均值最為常見。English name:(Mean)...
如果上市公司股份總額沒有發生變化,其年度每股收益就不存在加權平均的差異。這時就不必用加權平均法來計算公司的每股收益;但一些公司由於增發新股(含老股增發和新股...
一種是全麵攤薄淨資產收益率;另一種是加權平均淨資產收益率。不同的計算方法得出不同淨資產收益率指標結果,那么如何選擇計算淨資產收益率的方法就顯得尤為重要。 ...
