基本介紹
- 中文名:高斯整數環
- 外文名:ring of Gauss integers
- 類別:歐式環的一個著名例子
- 定義:Z[i]對通常數的加乘法構成個整環
- 一級學科:數學
- 二級學科:環與代數
- 類型:數學術語
簡介




基本性質



高斯整數環中素元的形成
Z[i]中的單位

Z[i]中的素元

Z[i]中的整數素元

Z[i]中的非整數素元

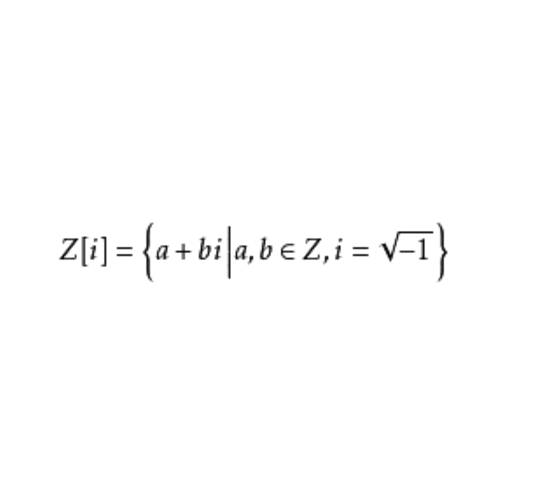











高斯整數環(ring of Gauss integers)是歐氏環的一個著名例子。設Z[i]={a+bi | a,b是整數,i為虛數單位}。 Z[i]對通常數的加法和乘法構成一個整環,稱為高斯整數環。而將a +bi → ...
高斯素數 1, −1, i及−i都是高斯整數環裡面的單位元。除此之外,在高斯整環裡面不能因子分解的數稱為高斯素數。高斯素數分為兩類,其中一類是形式為4n+3(n是整數)的普通素數,如3,7等,它們在高斯整環裡面也不能夠因子...
q:是既約元,則必有n=m,且適當調換次序後對於i=1,2, w,n均有p與,相伴,則稱R為單一分解環.整數環、單一分解環上多項式環都是單一分解環.庫默爾(Kummer, E.E.)於1944年首先指出整環Z[飛]不是單一分解環.整環是單一分解環...
高斯研究了復整數環的理論--即高斯整數。他在3次情形的費馬猜想中也用了擴環的代數數論性質。代數數論發展的一個里程碑,則是希爾伯特的《數論報告》。隨著數學工具的不斷深化, 數論開始和代數幾何深刻聯繫起來, 最終發展稱為當今最...
高斯整環唯一因子分解完整的答案使用費爾馬大定理,其結果為: 得出這種簡單的結果對更一般的整數環來說是代數數論的基本問題。當代數數域K是有理數Q的阿貝爾擴張時(即阿貝爾群的伽羅瓦擴張)類域論實現了這一目標。
高斯整數環 。域上的多項式環()與冪級數環(φ(f) 定義為使 的最大非負整數 n)。離散賦值環, φ(x)定義為使 的最大非負整數n,其中 表該離散賦值環的唯一極大理想。描述 在數學中,更具體地說在抽象代數和環論中,歐...
每個高斯整數都是代數數,所謂高斯整數,是形如 a+bi 的複數,其中 a 和 b 都是整數。因為 a+bi 是方程 (x²-a²+b²)²+4a²b²=0 的複數解。同理,實部和虛部都是代數數的複數也是代數數。當a是有理數時,...
一個元素是否為素元,取決於該元素處於哪個環內;例如,2在 Z 里是個素元,但在高斯整數環 Z[i] 里則不是,因為 2 = (1 + i)(1 - i) 且 2 無法整除等式右邊的任一因子。整環 一個環是一個集合 A 以及它上面的兩種...
1801年,C.F.高斯發表了他在20歲時所寫的數論著作《算術研究》,展現了他的一個傑出的思想,即把有理數域和有理整數環上的許多初等數論問題,放到更大的域和環──二次域和它的(代數)整數環上來研究。他在這些方面的工作,是...
18世紀末到19世紀中期,C.F.高斯和E.E.庫默爾等人在研究關於有理整數性質和方程的有理整數解的時候,把這些初等數論問題放在二次域、分圓域以及它們的代數整數環中考慮,經過J.W.R.戴德金和D.希爾伯特等人的抽象化和系統化,形成了...
此定理可推廣至更一般的交換代數和代數數論。高斯證明復整數環Z[i]也有唯一分解定理。它也誘導了諸如唯一分解整環,歐幾里得整環等等概念。 更一般的還有戴德金理想分解定理。素數等差數列 存在任意長度的素數等差數列。等差數列是數列的一種...
第2章環 2.1環的概念 2.2無零因子環 2.3理想和商環 2.4素理想和極大理想 2.5環的同態、商域 2.6唯一分解整環 2.7主理想整環和歐氏環 *2.8高斯整數環與二平方和問題 2.9多項式環 2.10唯一分解整環上的多項式環 第3章...
graphs of the ring Zn[i], 數學雜誌, 2016, 36 (4) : 676-682.[16] 韋揚江, 梁藝耀, 唐高華, 蘇磊磊, 陳蔚凝. 模 n 高斯整數環的商環的立方映射圖 , 廣西師範大學學報(自然科學版), 2016, 34 (3) : 53-61.
第2章 環和域 2.1 基本概念 2.2 環的同構定理 2.3 同態的套用 2.4 交換環中的因子分解 附錄2.1 高斯整數環與二平方和問題 2.5 多項式環 2.6 域的擴張 附錄2.2 對稱多項式 附錄2.3 代數基本定理的一個證明 附...
也是許多其他定理的邏輯支撐點和出發點。此定理可推廣至更一般的交換代數和代數數論。高斯證明復整數環Z[i]也有唯一分解定理。它也誘導了諸如唯一分解整環,歐幾里得整環等等概念,更一般的還有戴德金理想分解定理。
