人物生平 馮·諾依曼,著名匈牙利裔美籍數學家、計算機科學家、物理學家和化學家 。1903年12月28日生於匈牙利布達佩斯的一個猶太人家庭。
馮·諾依曼的父親麥克斯年輕有為、風度翩翩,憑著勤奮、機智和善於經營,年輕時就已躋身於布達佩斯的銀行家行列。馮·諾依曼的母親是一位善良的婦女,賢慧溫順,受過良好教育。
小時候的馮諾依曼 馮·諾依曼從小就顯示出數學和記憶方面的天才,從孩提時代起,馮諾依曼就有過目不忘的天賦,六歲時他就能用希臘語同父親互相開玩笑。六歲時他能心算做八位數除法,八歲時掌握微積分,在十歲時他花費了數月讀完了一部四十八卷的世界史,並可以對當前發生的事件和歷史上某個事件做出對比,並討論兩者的軍事理論和政治策略,十二歲就讀懂領會了波萊爾的大作《函式論》要義。
微積分 的實質是對無窮小量進行數學分析。人類探索有限、無限以及它們之間的關係由來已久,17世紀由牛頓萊布尼茨發現的微積分,是人類探索無限方面取得的一項激動人心的偉大成果。三百年來,它一直是高等學府的教學內容,隨著時代的發展,微積分在不斷地改變它的形式,概念變得精確了,基礎理論紮實了,甚至有不少簡明恰當的陳述。但不管怎么說,八歲的兒童要弄懂微積分,仍然是罕見的。上述種種傳聞雖然不盡可信,但馮·諾伊曼的才智過人,則是與他相識的人們的一致看法。
年輕時的馮·諾依曼 1914年夏天,約翰進入了大學預科班學習,是年7月28日,
奧匈帝國 藉故向塞爾維亞宣戰,揭開了第一次世界大戰的序幕。由於戰爭動亂連年不斷,馮·諾依曼全家離開過匈牙利,以後再重返布達佩斯。當然他的學業也會受到影響。但是在畢業考試時,馮·諾依曼的成績仍名列前茅(除體育和書寫外,都是A)。
1921年,馮·諾依曼通過“成熟”考試時,已被大家當作數學家了。他的第一篇論文是和菲克特合寫的,那時他還不到18歲。
麥克斯 由於考慮到經濟上原因,請人勸阻年方17的馮·諾依曼不要專攻數學,後來父子倆達成協定,馮·諾依曼便去攻讀化學。
其後的四年間,馮·諾依曼在
布達佩斯大學 註冊為數學方面的學生,但並不聽課,只是每年按時參加考試,考試都得A。與此同時,馮·諾依曼進入柏林大學(1921年),1923年又進入瑞士蘇黎世聯邦工業大學學習化學。1926年他在
蘇黎世聯邦工業大學 獲得化學方面的大學畢業學位,通過在每學期期末回到
布達佩斯大學 通過課程考試,他也獲得了
布達佩斯大學 數學博士學位。
馮·諾依曼的這種不參加聽課只參加考試的求學方式,當時是非常特殊的,就整個歐洲來說也是完全不合規則的。但是這不合規則的學習方法,卻又非常適合馮·諾依曼。
逗留在蘇黎世期間,馮·諾依曼常常利用空餘時間研讀數學、寫文章和數學家通信。在此期間馮·諾依曼受到了希爾伯特和他的學生
施密特 和外爾的思想影響,開始研究
數理邏輯 。當時外爾和
波伊亞 兩位也在蘇黎世,他和他們有過交往。一次外爾短期離開蘇黎世,馮·諾依曼還代他上過課。聰慧加上得天獨厚的栽培,馮·諾依曼在茁壯地成長,當他結束學生時代的時候,他已經漫步在數學、物理、化學三個領域的某些前沿。
1926年春,馮·諾依曼到
哥廷根大學 任
希爾伯特 的助手。1927~1929年,馮·諾依曼在柏林大學任兼職講師,期間他發表了集合論、代數和量子理論方面的文章。1927年馮·諾依曼到波蘭里沃夫出席數學家會議,那時他在數學基礎和集合論方面的工作已經很有名氣。
約翰·馮·諾依曼 1929年,馮·諾依曼轉任漢堡大學兼職講師。1930年他首次赴美,成為普林斯頓大學的客座講師。善於匯集人才的美國不久就聘馮·諾依曼為客座教授。
馮諾依曼在講課(“用黑板擦證明定理”) 馮·諾依曼曾經算過,德國大學裡現有的和可以期待的空缺很少,照他典型的推理得出,在三年內可以得到的教授任命數是三,而參加競爭的講師則有40名之多。在普林斯頓,馮·諾依曼每到夏季就回歐洲,一直到1933年擔任普林斯頓高級研究院教授為止。當時高級研究院聘有六名教授,其中就包括愛因斯坦,而年僅30歲的馮·諾依曼是他們當中最年輕的一位。
在高等研究院初創時間,歐洲來訪者會發現,那裡充滿著一種極好的不拘禮節的、濃厚的研究風氣。教授們的辦公室設定在大學的“優美大廈”里,生活安定,思想活躍,高質量的研究成果層出不窮。可以這樣說,那裡集中了有史以來最多的有數學和物理頭腦的人才。
1930年馮·諾依曼和瑪麗達·柯維斯結婚。1935年他們的女兒
瑪麗娜 出生在普林斯頓。馮·諾依曼家裡常常舉辦時間持續很長的社交聚會,這是遠近皆知的。1937年馮·諾依曼與妻子離婚,1938年又與克拉拉·丹結婚,並一起回到普林斯頓。丹隨馮·諾依曼學數學,後來成為優秀的程式編制家。與克拉拉婚後,馮·諾依曼的家仍是科學家聚會的場所,還是那樣殷勤好客,在那裡人人都會感到一種聰慧的氣氛。
馮諾依曼和妻子克拉拉 二次大戰歐洲戰事爆發後,馮·諾依曼的活動超越了普林斯頓,參與了同反法西斯戰爭有關的多項科學研究計畫。1943年起他成了製造核子彈的顧問,戰後仍在政府諸多部門和委員會中任職。1954年又成為美國原子能委員會成員。
馮·諾依曼的多年老友,原子能委員會主席
史特勞斯 曾對他作過這樣的評價:從他被任命到1955年深秋,馮·諾依曼幹得很漂亮。他有一種使人望塵莫及的能力,最困難的問題到他手裡。都會被分解成一件件看起來十分簡單的事情,用這種辦法,他大大地促進了原子能委員會的工作。
馮·諾依曼的健康狀況一直很好,可是由於工作繁忙,到1954年他開始感到十分疲勞。
艾森豪為馮·諾依曼頒獎 1955年的夏天,X射線檢查出他患有癌症,但他還是不停的工作,病勢擴展。後來他被安置在輪椅上,繼續思考、演說及參加會議。長期而無情的疾病折磨著他,慢慢地終止了他所有的活動。1956年4月,他進入華盛頓的沃爾特·里德醫院,1957年2月8日在醫院逝世,享年53歲。
個人成就 馮·諾伊曼是二十世紀最重要的數學家之一,在純粹數學和套用數學方面都有傑出的貢獻。他的工作大致可以分為兩個時期:1940年以前,主要是純粹數學的研究:在數理邏輯方面提出簡單而明確的序數理論,並對集合論進行新的公理化,其中明確區別集合與類;其後,他研究
希爾伯特空間 上線性自伴運算元譜理論,從而為量子力學打下數學基礎;1930年起,他證明平均遍歷定理開拓了遍歷理論的新領域;1933年,他運用緊緻群解決了希爾伯特第五問題;此外,他還在測度論、格論和連續幾何學方面也有開創性的貢獻;從1936~1943年,他和默里合作,創造了運算元環理論,即所謂的馮·諾伊曼代數。
1940年以後,馮·諾伊曼轉向套用數學。如果說他的純粹數學成就屬於數學界,那么他在力學、經濟學、數值分析和電子計算機方面的工作則屬於全人類。第二次世界大戰開始,馮·諾伊曼因戰事的需要研究可壓縮氣體運動,建立衝擊波理論和湍流理論,發展了流體力學;從1942年起,他同
莫根施特恩 合作,寫作《博弈論和經濟行為》一書,這是博弈論(又稱對策論)中的經典著作,使他成為數理經濟學的奠基人之一。
馮·諾伊曼對世界上第一台電子計算機ENIAC(電子數字積分計算機)的設計提出過建議,1945年3月他在共同討論的基礎上起草了一個全新的“存儲程式通用電子計算機方案”--
EDVAC (Electronic Discrete Variable Automatic Computer的縮寫)。這對後來計算機的設計有決定性的影響,特別是確定計算機的結構,採用存儲程式以及二進制編碼等,至今仍為電子計算機設計者所遵循。
1946年,馮·諾依曼開始研究程式編制問題,他是現代數值分析——計算數學的締造者之一,他首先研究線性代數和算術的數值計算,後來著重研究非線性微分方程的離散化以及穩定問題,並給出誤差的估計。他協助發展了一些算法,特別是
蒙特卡羅方法 。
40年代末,他開始研究自動機理論,研究一般邏輯理論以及自複製系統。在生命的最後時刻他深入比較天然自動機與人工自動機。他逝世後其未完成的手稿在1958年以《
計算機與人腦 》為名出版。
馮·諾伊曼的主要著作收集在《馮·諾伊曼全集》(6卷,1961)中。
無論在純粹數學還是在套用數學研究方面,馮·諾依曼都顯示了卓越的才能,取得了眾多影響深遠的重大成果。不斷變換研究主題,常常在幾種學科交叉滲透中獲得成就是他的特色。
簡單來說他的精髓貢獻是兩點:2進制思想與程式記憶體思想。
回顧20世紀科學技術的輝煌發展時,不能不提及20世紀最傑出的數學家之一的
馮·諾依曼 。眾所周知,1946年發明的
電子計算機 ,大大促進了科學技術的進步,大大促進了社會生活的進步。鑒於馮·諾依曼在發明電子計算機中所起到關鍵性作用,他被西方人譽為“計算機之父”。而在經濟學方面,他也有突破性成就,被譽為“
博弈論 之父”。在物理領域,馮·諾依曼在30年代撰寫的《量子力學的數學基礎》已經被證明對
原子物理學 的發展有極其重要的價值。在化學方面也有相當的造詣,曾獲蘇黎世高等技術學院化學系大學學位。與同為
猶太人 的
哈耶克 一樣,他無愧是上世紀最偉大的
全才 之一。
馮·諾依曼(右)等在世界上第一台計算機前 馮·諾依曼在數學的諸多領域都進行了開創性工作,並作出了重大貢獻。在第二次世界大戰前,他主要從事運算元理論、
集合論 等方面的研究。1923年關於集合論中超限序數的論文,顯示了馮·諾依曼處理集合論問題所特有的方式和風格。他把集會論加以公理化,他的公理化體系奠定了公理集合論的基礎。他從公理出發,用
代數 方法導出了集合論中許多重要概念、基本運算、重要定理等。特別在1925年的一篇論文中,馮·諾依曼就指出了任何一種公理化系統中都存在著無法判定的
命題 。
1933年,馮·諾依曼解決了
希爾伯特 第5問題,即證明了局部歐幾里得緊群是李群。1934年他又把緊群理論與波爾的
殆周期函式 理論統一起來。他還對一般拓撲群的結構有深刻的認識,弄清了它的代數結構和
拓撲 結構與
實數 是一致的。他對運算元代數進行了開創性工作,並奠定了它的理論基礎,從而建立了運算元代數這門新的數學分支。這個分支在當代的有關數學文獻中均稱為馮·諾依曼代數。這是有限維空間中矩陣代數的自然推廣。馮·諾依曼還創立了
博弈論 這一現代數學的又一重要分支。1944年發表了奠基性的重要論文《博弈論與經濟行為》。論文中包含博弈論的
純粹數學 形式的闡述以及對於實際博弈套用的詳細說明。文中還包含了諸如
統計理論 等教學思想。馮·諾依曼在
格論 、連續幾何、
理論物理 、動力學、
連續介質力學 、氣象計算、
原子能 和經濟學等領域都作過重要的工作。
馮·諾依曼對人類的最大貢獻是對計算機科學、計算機技術、
數值分析 和經濟學中的博弈論的開拓性工作。
一般認為
ENIAC 機是世界第一台電子計算機,它是由美國科學家研製的,於1946年2月14日在
費城 開始運行。其實由湯米、費勞爾斯等英國科學家研製的“
科洛薩斯 ”計算機比ENIAC機問世早兩年多,於1944年1月10日在布萊奇利園區開始運行。ENIAC機證明電子真空技術可以大大地提高計算技術,不過,ENIAC機本身存在兩大缺點:(1)沒有
存儲器 ;(2)它用布線接板進行控制,甚至要搭接幾天,計算速度也就被這一工作抵消了。ENIAC機研製組的莫克利和
埃克特 顯然是感到了這一點,他們也想儘快著手研製另一台計算機,以便改進。
1944年,諾伊曼參加
核子彈 的研製工作,該工作涉及到極為困難的計算。在對原子核反應過程的研究中,要對一個反應的傳播做出“是”或“否”的回答。解決這一問題通常需要通過幾十億次的數學運算和邏輯指令,儘管最終的數據並不要求十分精確,但所有的中間運算過程均不可缺少,且要儘可能保持準確。他所在的洛·斯阿拉莫斯實驗室為此聘用了一百多名女計算員,利用台式計算機從早到晚計算,還是遠遠不能滿足需要。無窮無盡的數字和邏輯指令如同沙漠一樣把人的智慧和精力吸盡。
被計算機所困擾的諾伊曼在一次極為偶然的機會中知道了ENIAC計算機的研製計畫,從此他投身到計算機研製這一宏偉的事業中,建立了一生中最大的豐功偉績。
1944年夏的一天,正在火車站候車的諾伊曼巧遇戈爾斯坦,並同他進行了短暫的交談。當時,戈爾斯坦是美國彈道實驗室的軍方負責人,他正參與ENIAC計算機的研製工作。在交談中,戈爾斯坦告訴了諾伊曼有關ENIAC的研製情況。具有遠見卓識的諾伊曼為這一研製計畫所吸引,他意識到了這項工作的深遠意義。
馮·諾依曼和奧本海默在第一台計算機前合影 馮·諾依曼由ENIAC機研製組的戈爾德斯廷
中尉 介紹參加ENIAC機研製小組後,便帶領這批富有創新精神的年輕科技人員,向著更高的目標進軍。1945年,他們在共同討論的基礎上,發表了一個全新的“存儲程式通用電子計算機方案”--
EDVAC (Electronic Discrete Variable Automatic Computer的縮寫)。在這過程中,馮·諾依曼顯示出他雄厚的數理基礎知識,充分發揮了他的顧問作用及探索問題和綜合分析的能力。諾伊曼以“關於EDVAC的報告草案”為題,起草了長達101頁的總結報告。報告廣泛而具體地介紹了製造電子計算機和程式設計的新思想。這份報告是計算機發展史上一個劃時代的文獻,它向世界宣告:電子計算機的時代開始了。
EDVAC方案明確奠定了新機器由五個部分組成,包括:
運算器 、控制器、
存儲器 、輸入和輸出設備,並描述了這五部分的職能和相互關係。報告中,諾伊曼對EDVAC中的兩大設計思想作了進一步的論證,為計算機的設計樹立了一座里程碑。
設計思想之一是
二進制 ,他根據電子元件雙穩工作的特點,建議在電子計算機中採用二進制。報告提到了二進制的優點,並預言,二進制的採用將大大簡化機器的邏輯線路。
計算機基本工作原理是存儲程式和程式控制,它是由世界著名數學家馮·諾依曼提出的。美籍匈牙利數學家馮·諾依曼被稱為“計算機之父”。
實踐證明了諾伊曼預言的正確性。如今,
邏輯代數 的套用已成為設計電子計算機的重要手段,在EDVAC中採用的主要邏輯線路也一直沿用著,只是對實現邏輯線路的工程方法和邏輯電路的分析方法作了改進。
經典理論 馮諾依曼體系結構
說到計算機的發展,就不能不提到美國科學家馮諾依曼。從20世紀初,物理學和電子學科學家們就在爭論製造可以進行數值計算的機器應該採用什麼樣的結構。人們被十進制這個人類習慣的計數方法所困擾。所以,那時以研製
模擬計算機 的呼聲更為響亮和有力。20世紀30年代中期,美國科學家馮諾依曼大膽的提出,拋棄十進制,採用二進制作為
數字計算機 的數制基礎。同時,他還說預先編制計算程式,然後由計算機來按照人們事前制定的計算順序來執行數值計算工作。
馮諾依曼理論的要點是:數字計算機的數制採用二進制;計算機應該按照程式順序執行。
人們把馮諾依曼的這個理論稱為
馮諾依曼體系結構 。從ENIAC(ENIAC並不是馮諾依曼體系)到當前最先進的計算機都採用的是馮諾依曼體系結構。所以馮諾依曼是當之無愧的數字計算機之父。
根據馮諾依曼體系結構構成的計算機,必須具有如下功能:
把需要的程式和數據送至計算機中。
必須具有長期記憶程式、數據、中間結果及最終運算結果的能力。
能夠完成各種算術、
邏輯運算 和數據傳送等數據加工處理的能力。
能夠根據需要控制程式走向,並能根據指令控制機器的各部件協調操作。
能夠按照要求將處理結果輸出給用戶。
為了完成上述的功能,計算機必須具備五大基本組成部件,包括:
輸入數據和程式的輸入設備
記憶程式和數據的存儲器
完成數據加工處理的運算器
控制程式執行的控制器
輸出處理結果的輸出設備
理論基礎 馮·諾依曼的第一篇論文是和菲克特合寫的,是關於
切比雪夫 多項式求根法的菲葉定理推廣,註明的日期是1922年,那時馮·諾依曼還不滿18歲。另一篇文章討論一致稠密數列,用匈牙利文寫就,題目的選取和證明手法的簡潔顯露出馮·諾依曼在代數技巧和集合論直觀結合的特徵。
1923年當馮·諾依曼還是蘇黎世的大學生時,發表了超限序數的論文。文章第一句話就直率地聲稱“本文的目的是將康托的序數概念具體化、精確化”。他的關於序數的定義,已被普遍採用。
強烈企求探討公理化是馮·諾依曼的願望,大約從l925年到l929年,他的大多數文章都嘗試著貫徹這種公理化精神,以至在理論物理研究中也如此。當時,他對集合論的表述處理,尤感不夠形式化,在他1925年關於集合論公理系統的博士論文中,開始就說“本文的目的,是要給集合論以邏輯上無可非議的公理化論述”。
有趣的是,馮·諾依曼在論文中預感到任何一種形式的公理系統所具有的局限性,模糊地使人聯想到後來由
哥德爾證明 的不完全性定理。對此文章,著名
邏輯學家 、公理集合論奠基人之一的
弗蘭克爾 教授曾作過如下評價:“我不能堅持說我已把(文章的)一切理解了,但可以確有把握地說這是一件傑出的工作,並且透過他可以看到一位巨人”。
1928年馮·諾依曼發表了論文《集合論的公理化》,是對上述集合論的公理化處理。該系統十分簡潔,它用第一型對象和第二型對象相應表示樸素集合論中的集合和集合的性質,用了一頁多一點的紙就寫好了系統的公理,它已足夠建立樸素集合論的所有內容,並藉此確立整個現代數學。
馮·諾依曼的系統給出了集合論的也許是第一個基礎,所用的有限條公理,具有像初等幾何那樣簡單的
邏輯結構 。馮·諾依曼從公理出發,巧妙地使用代數方法導出集合論中許多重要概念的能力簡直叫人驚嘆不已,所有這些也為他未來把興趣落腳在計算機和“機械化”證明方面準備了條件。
20年代後期,馮·諾依曼參與了希爾伯特的元數學計畫,發表過幾篇證明部分算術公理無矛盾性的論文。l927年的論文《關於希爾伯特證明論》最為引人注目,它的主題是討論如何把數學從矛盾中解脫出來。文章強調由希爾伯特等提出和發展的這個問題十分複雜,當時還未得到滿意的解答。它還指出
阿克曼 排除矛盾的證明並不能在古典分析中實現。為此,馮·諾依曼對某個子系統作了嚴格的有限性證明。這離希爾伯特企求的最終解答似乎不遠了。恰在此時,1930年哥德爾證明了不完全性定理。定理斷言:在包含初等算術(或集合論)的無矛盾的
形式系統 中,系統的無矛盾性在系統內是不可證明的。至此,馮·諾依曼只能中止這方面的研究。
馮·諾依曼還得到過有關集合論本身的專門結果。他在數學基礎和集合論方面的興趣一直延續到他生命的結束。
純粹數學 在1930~1940年間,馮·諾依曼在純粹數學方面取得的成就更為集中,創作更趨於成熟,聲譽也更高漲。後來在一張為國家科學院填的問答表中,馮·諾依曼選擇了量子理論的數學基礎、運算元環理論、各態遍歷定理三項作為他最重要數學工作。
1927年馮·諾依曼已經在量子力學領域內從事研究工作。他和希爾伯特以及諾戴姆聯名發表了論文《量子力學基礎》。該文的基礎是希爾伯特1926年冬所作的關於量子力學新發展的講演,諾戴姆幫助準備了講演,馮·諾依曼則從事於該主題的數學形式化方面的工作。文章的目的是將
經典力學 中的精確
函式關係 用機率關係代替之。希爾伯特的元數學、公理化的方案在這個生氣勃勃的領域裡獲得了施展,並且獲得了理論物理和對應的數學體系間的同構關係。對這篇文章的歷史重要性和影響無論如何評價都不會過高。馮·諾依曼在文章中還討論了物理學中可觀察算符的運算的輪廓和
埃爾米特 運算元的性質,無疑,這些內容構成了《量子力學的數學基礎》一書的序曲。
1932世界聞名的
斯普林 格出版社出版了他的《量子力學的數學基礎》,它是馮·諾依曼主要著作之一,初版為德文,1943年出了法文版,1949年為西班牙文版,1955年被譯成英文出版,至今仍不失為這方面的經典著作。當然他還在量子統計學、量子熱力學、引力場等方面做了不少重要工作。
客觀地說,在量子力學發展史上,馮·諾依曼至少作出過兩個重要貢獻:狄拉克對量子理論的數學處理在某種意義下是不夠嚴格的,馮·諾依曼通過對無界運算元的研究,發展了希爾伯特運算元理論,彌補了這個不足;此外,馮·諾依曼明確指出,量子理論的統計特徵並非由於從事測量的觀察者之狀態未知所致。藉助於希爾伯特空間運算元理論,他證明凡包括一般物理量締合性的量子理論之假設,都必然引起這種結果。
對於馮·諾依曼的貢獻,
諾貝爾物理學獎 獲得者威格納曾作過如下評價:“在量子力學方面的貢獻,就是以確保他在當代物理學領域中的特殊地位。”
在馮·諾依曼的工作中,希爾伯特空間上的運算元譜論和運算元環論占有重要的支配地位,這方面的文章大約占了他發表的論文的三分之一。它們包括對線性運算元性質的極為詳細的分析,和對無限維空間中運算元環進行代數方面的研究。
運算元環理論始於1930年下半年,馮·諾依曼十分熟悉
諾特 和阿丁的非
交換代數 ,很快就把它用於希爾伯特空間上
有界線性運算元 組成的代數上去,後人把它稱之為馮·諾依曼運算元代數。
1936~1940年間,馮·諾依曼發表了六篇關於非交換運算元環論文,可謂20世紀分析學方面的傑作,其影響一直延伸至今。馮·諾依曼曾在《量子力學的數學基礎》中說過:由希爾伯特最早提出的思想就能夠為物理學的量子論提供一個適當的基礎,而不需再為這些物理理論引進新的數學構思。他在運算元環方面的研究成果應驗了這個目標。馮·諾依曼對這個課題的興趣貫穿了他的整個生涯。
運算元環理論的一個驚人的生長點是由馮·諾依曼命名的連續幾何。普通幾何學的維數為整數1、2、3等,馮·諾依曼在著作中已看到,決定一個空間的維數結構的,實際上是它所容許的旋轉群。因而維數可以不再是整數,連續級數空間的幾何學終於提出來了。
1932年,馮·諾依曼發表了關於遍歷理論的論文,解決了遍歷定理的證明,並用運算元理論加以表述,它是在統計力學中遍歷假設的嚴格處理的整個研究領域中,獲得的第一項精確的數學結果。馮·諾依曼的這一成就,可能得再次歸功於他所嫻熟掌握的受到集合論影響的數學分析方法,和他自己在希爾伯特運算元研究中創造的那些方法。它是20世紀數學分析研究領域中取得的最有影響成就之一,也標誌著一個數學物理領域開始接近精確的現代分析的一般研究。
此外馮·諾依曼在實變函式論、測度論、拓撲、連續群、格論等數學領域也取得不少成果。1900年希爾伯特在那次著名的演說中,為20世紀
數學研究 提出了23個問題,馮·諾依曼也曾為解決希爾伯特第五問題作了決定性貢獻。
套用數學 1940年,是馮·諾依曼科學生涯的一個轉換點。在此之前,他是一位通曉物理學的登峰造極的純粹數學家;此後則成了一位牢固掌握純粹數學的出神入化的套用數學家。他開始關注當時把數學套用於物理領域去的最主要工具——
偏微分方程 。研究同時他還不斷創新,把非古典數學套用到兩個新領域:對策論和電子計算機。
馮·諾依曼的這個轉變一方面來自他長期對數學物理問題的鐘情;另一方面來自當時社會方面的需要。第二次世界大戰爆發後,馮·諾依曼應召參與了許多軍事科學研究計畫和工程項目。1940~1957年任馬里蘭
阿伯丁 試驗彈道研究實驗室科學顧問;1941~1955年在華盛頓海軍軍械局;1943~1955年任洛斯·阿拉莫斯實驗室顧問;1950~1955年,陸軍特種武器設計委員會委員;1951~1957年。美國空軍華盛頓科學顧問委員會成員;1953~1957年,原子能技術顧問小組成員;1954~1957年,飛彈顧問委員會主席。
馮·諾依曼研究過連續介質力學。很久以來,他對
湍流現象 一直感興趣。l937年他關注納維—斯克克斯方程的統計處理可能性的討論,1949年他為海軍研究部寫了《湍流的最新理論》。
馮·諾依曼研究過
激波 問題。他在這個領域中的大部分工作,直接來自國防需要。他在碰撞激波的相互作用方面貢獻引人注目,其中有一結果,是首先嚴格證明了恰普曼—儒格假設,該假設與激波所引起的燃燒有關。關於激波反射理論的系統研究由他的《激波理論進展報告》開始。
馮·諾依曼研究過氣象學。有相當一段時間,地球大氣運動的流體力學方程組所提出的極為困難的問題一直吸引著他。隨著電子計算機的出現,有可能對此問題作數值研究分析。馮·諾依曼搞出的第一個高度規模化的計算,處理的是一個二維模型,與地轉近似有關。他相信人們最終能夠了解、計算並實現控制以致改變氣候。
馮·諾依曼還曾提出用聚變引爆核燃料的建議,並支持發展氫彈。1947年軍隊發嘉獎令,表揚他是物理學家、工程師、武器設計師和愛國主義者。
博弈論 馮·諾依曼不僅曾將自己的才能用於武器研究等,而且還用於社會研究。1928年,
馮·諾依曼 證明了
博弈論 的基本原理,從而宣告了博弈論的正式誕生。由他創建的對策論,無疑是他在套用數學方面取得的最為令人羨慕的傑出成就。現今,博弈論主要指研究社會現象的特定
數學方法 。它的基本思想,就是分析多個主體之間的利害關係時,重視在諸如下棋、玩撲克牌等室內遊戲中競賽者之間的討價還價,交涉,結夥,利益分配等行為方式的類似性。
馮諾依曼和摩根斯特恩 博弈論的一些想法,20年代初就曾有過,真正的創立還得從馮·諾依曼1928年關於社會博弈理論的論文算起。在這篇文章中,他證明了最小最大定理,這個定理用於處理一類最基本的二人對策問題。如果對策雙方中的任何一方,對每種可能的策略,考慮了可能遭到的最大損失,從而選擇“最大損失”最小的一種為“最優”策略,那么從統計角度來看,他就能夠確保方案是最佳的。這方面的工作大致已達到完善。在同一篇論文中,馮·諾依曼也明確表述了n個遊戲者之間的一般對策。
博弈論也被用於經濟學。經濟理論中的數學研究方法,大致可分為定性研究為目標的純粹理論和以實證的、統計的研究為目標的計量經濟學。前者稱為數理經濟學,正式確立於20世紀40年代之後。無論在思想上或方法上,都明顯地受到對策論的影響。
數理經濟學,過去模仿經典數學物理的技巧,所用的
數學工具 主要是微積分和微分方程、將經濟問題當成經典力學問題處理。顯然,幾十個商人參加的貿易洽談會,用經典數學分析處理,其複雜程度遠遠超過
太陽系行星 的運動,這種方法的效果往往很難是預期的。馮·諾依曼毅然放棄這種簡單的機械類比,代之以新穎的博弈論觀點和新的數學—和凸性的思想。
1944年,馮·諾依曼和
摩根 斯特恩合著的《博弈論和經濟行為》是這方面的奠基性著作。將二人博弈推廣到n人博弈結構並將博弈論系統的套用於經濟領域,從而奠定了這一學科的基礎和理論體系。論文包含了博弈論的純粹數學形式的闡述以及對於實際套用的詳細說明。這篇論文以及所作的與某些經濟理論的基本問題的討論,引起了對經濟行為和某些社會學問題的各種不同研究,時至今日,這已是套用廣泛、羽毛日益豐盛的一門數學學科。有些科學家熱情頌揚它可能是“20世紀前半期最偉大的科學貢獻之一”。
計算機 對馮·諾依曼聲望有所貢獻的最後一個課題是電子計算機和自動化理論。
早在
洛斯阿拉莫斯 ,馮·諾依曼就明顯看到,即使對一些理論物理的研究,只是為了得到定性的結果,單靠解析研究也已顯得不夠,必須輔之以數值計算。進行手工計算或使用台式計算機所需花費的時間是令人難以容忍的,於是馮·諾依曼勁頭十足的開始從事電子計算機和計算方法的研究。
1944~1945年間,馮·諾依曼形成了現今所用的將一組
數學過程 轉變為計算機指令語言的基本方法,當時的電子計算機(如ENIAC)缺少靈活性、普適性。馮·諾依曼關於機器中的固定的、普適線路系統,關於“流圖”概念,關於“代碼”概念為克服以上缺點作出了重大貢獻。儘管對數理邏輯學家來說,這種安排是顯見的。
計算機工程的發展也應大大歸功於馮·諾依曼。計算機的邏輯
圖式 ,現代計算機中存儲、速度、基本指令的選取以及線路之間相互作用的設計,都深深受到馮·諾依曼思想的影響。他不僅參與了電子管元件的計算機
ENIAC 的研製,並且還在
普林斯頓高等研究院 親自督造了一台計算機。稍前,馮·諾依曼還和摩爾小組一起,寫出了一個全新的存貯程式通用電子計算機方案EDVAC,長達101頁的報告轟動了數學界。這一向專搞理論研究的普林斯頓高等研究院也批准讓馮·諾依曼建造計算機,其依據就是這份報告。
速度超過人工計算千萬倍的電子計算機,不僅極大地推動數值分析的進展,而且還在數學分析本身的基本方面,刺激著嶄新的方法的出現。其中,由馮·諾依曼等制訂的使用隨機數處理確定性數學問題的
蒙特卡洛法 的蓬勃發展,就是突出的實例。
19世紀那種數學物理原理的精確的數學表述,在現代物理中似乎十分缺乏。基本粒子研究中出現的紛繁複雜的結構,令人眼花繚亂,要想很快找到數學綜合理論希望還很渺茫。單從綜合角度看,且不提在處理某些偏微分方程時所遇到的分析困難,要想獲得精確解希望也不大。所有這些都迫使人們去尋求能藉助電子計算機來處理的新的數學模式。馮·諾依曼為此貢獻了許多天才的方法:它們大多分載在各種實驗報告中。從求解偏微分方程的數值近似解,到長期天氣數值預報,以至最終達到控制氣候等。
在馮·諾依曼生命的最後幾年,他的思想仍甚活躍,他綜合早年對邏輯研究的成果和關於計算機的工作,把眼界擴展到一般自動機理論。他以特有的膽識進擊最為複雜的問題:怎樣使用不可靠元件去設計可靠的自動機,以及建造自己能再生產的自動機。從中,他意識到計算機和人腦機制的某些類似,這方面的研究反映在西列曼講演中;逝世後才有人以《計算機和人腦》的名字,出了單行本。儘管這是未完成的著作,但是他對人腦和計算機系統的精確分析和比較後所得到的一些定量成果,仍不失其重要的學術價值。
主要著作 《經典力學的運算元方法》
《量子力學的數學基礎》(1932年)
馮·諾依曼逝世後,未完成的手稿於1958年以《計算機與人腦》為名出版。他的主要著作收集在六卷《馮·諾依曼全集》中,1961年出版。
另外,馮·諾依曼40年代出版的著作《博弈論和經濟行為》(與摩根斯頓合著),使他在經濟學和
決策科學 領域豎起了一塊豐碑。他被經濟學家公認為博弈論之父。當時年輕的
約翰·納什 在普林斯頓求學期間開始研究發展這一領域,並在1994年憑藉對博弈論的突出貢獻獲得了
諾貝爾經濟學獎 。
《 程式記憶體》是諾伊曼的另一傑作。通過對ENIAC的考察,諾伊曼敏銳地抓住了它的最大弱點--沒有真正的存儲器。ENIAC只在20個暫存器,它的程式是外插型的,指令存儲在計算機的其他電路中。這樣,解題之前,必需先想好所需的全部指令,通過手工把相應的電路
聯通 。這種準備工作要花幾小時甚至幾天時間,而計算本身只需幾分鐘。計算的高速與程式的手工存在著很大的矛盾。
針對這個問題,諾伊曼提出了程式記憶體的思想:把運算程式存在機器的
存儲器 中,程式設計員只需要在存儲器中尋找運算指令,機器就會自行計算,這樣,就不必每個問題都重新編程,從而大大加快了運算進程。這一思想標誌著自動運算的實現,標誌著電子計算機的成熟,已成為電子計算機設計的基本原則。
1946年7,8月間,馮·諾依曼和戈爾德斯廷、勃克斯在ENIAC方案的基礎上,為普林斯頓大學高級研究所研製IAS計算機時,又提出了一個更加完善的設計報告《電子計算機邏輯設計初探》.以上兩份既有理論又有具體設計的檔案,首次在全世界掀起了一股“計算機熱”,它們的綜合設計思想,便是著名的“馮·諾依曼機”,其中心就是有存儲程式原則--指令和數據一起存儲(存儲機)。這個概念被譽為“計算機發展史上的一個里程碑”。它標誌著電子計算機時代的真正開始,指導著以後的計算機設計。自然一切事物總是在發展著的,隨著科學技術的進步,今天人們又認識到“馮·諾依曼機”的不足,它妨礙著計算機速度的進一步提高,而提出了“非馮·諾依曼機”的構想。
馮·諾依曼還積極參與了推廣套用計算機的工作,對如何編製程序及搞數值計算都作出了傑出的貢獻。馮·諾依曼於1937年獲美國數學會的波策獎;1938年獲得博謝紀念獎;1947年獲美國總統的功勳獎章、美國海軍優秀公民服務獎;1956年獲
美國總統 的自由獎章和
費米獎 。
逸聞 1. 一次,在一個數學聚會上,有一個年輕人興沖沖的找到他,向他求教一個問題,他看了看就報出了正確答案。年輕人高興地請求他告訴自己簡便方法,並抱怨其他數學家用無窮級數求解的繁瑣。馮·諾依曼卻說道:“你誤會了,我正是用無窮級數求出的。”可見他擁有過人的心算能力。
2.據說有一天,馮·諾依曼心神不定地被同事拉上了牌桌。一邊打牌,一邊還在想他的課題,狼狽不堪地“輸掉”了10元錢。這位同事也是數學家,突然心生一計,想要捉弄一下他的朋友,於是用贏得的5元錢,購買了一本馮·諾依曼撰寫的《博弈論和經濟行為》,並把剩下的5元貼在書的封面,以表明他 “戰勝”了“賭博經濟理論家”,著實使馮·諾依曼“好沒面子”。
3.在ENIAC計算機研製時期。 有幾個數學家聚在一起切磋
數學難題 ,百思不得某題之解。有個人決定帶著台式計算器回家繼續演算。次日清晨,他眼圈黑黑,面帶倦容走進辦公室,頗為得意地對大家炫耀說:“我從昨天晚上一直算到今晨4點半,總算找到那難題的5種特殊解答。它們一個比一個更難咧!”說話間,馮·諾依曼推門進來,“什麼題更難?”雖只聽到後面半句話,但“更難”二字使他馬上來了勁。有人把題目講給他聽,教授頓時把自己該辦的事拋在爪哇國,興致勃勃地提議道:“讓我們一起算算這5種特殊的解答吧。”
大家都想見識一下教授的“神算”本領。只見馮·諾依曼眼望天花板,不言不語,迅速進到“入定” 狀態。約莫過了5分來鐘,就說出了前4種解答,又在沉思著第5種……。青年數學家再也忍不住了,情不自禁脫口講出答案。馮·諾依曼吃了一驚,但沒有接話茬。又過了1分鐘,他才說道:“你算得對!”
那位數學家懷著崇敬的心情離去,他不無揶揄地想:“還造什麼計算機喲,教授的頭腦不就是一台‘超高速計算機’嗎?”然而,馮·諾依曼卻呆在原地,陷入苦苦的思索,許久都不能自拔。有人輕聲向他詢問緣由,教授不安地回答說:“我在想,他究竟用的是什麼方法,這么快就算出了答案。”聽到此言,大家不禁哈哈大笑:“他用台式計算器算了整整一個夜晚!”馮·諾依曼一愣,也跟著開懷大笑起來。
4.馮諾依曼的駕駛水平很爛,經常發生事故,有一次他撞壞了車頭,在警局裡解釋道:“我正在路上正常駕駛,右方窗外的樹正在以60英里每小時的速度從我車旁穿過,突然,一棵樹站在了我的車前,咚!”
5.在馮諾依曼臨去世的前幾天,腫瘤已經占據了他的大腦,但記憶力有時還是不可思議得好,那天烏拉姆坐在他的病榻前用希臘語朗誦一本修昔底德書中他特別喜歡的亞丁人進攻梅洛思的故事和佩里萊的演說,他記得很牢,會糾正烏拉姆的錯誤和發音。
社會評價 認知能力 Hans Bethe(諾貝爾獎物理學獲得者):I have sometimes wondered whether a brain like von Neumann's does not indicate a species superior to that of man.(我有時在思考馮諾伊曼這樣的大腦是否暗示著存在比人類更高級的生物物種。)
David Blackwell:He was a really remarkable man.He listened to me talk about this rather obscure subject and in ten minutes he knew more about it than I did.He was extremely quick.(他是個出類拔萃的人,我給他大概地講了一下我最近研究的課題,在十分鐘之後他已經比我知道的更多了。他的思維真的是異常的敏捷。)
George Pólya:The only student of mine I was ever intimidated by. He was so quick.There was a seminar for advanced students in Zürich that I was teaching and von Neumann was in the class. I came to a certain theorem, and I said it is not proved and it may be difficult. Von Neumann didn't say anything but after five minutes he raised his hand. When I called on him he went to the blackboard and proceeded to write down the proof.After that I was afraid of von Neumann.(他是唯一的令我感到自己的教師地位受到威脅的學生,他實在是太敏銳了.有一次我在蘇黎世為研究生們作演講,當時馮諾依曼也在聽課,我提出了一個懸而未決的問題,過了5分鐘馮諾依曼舉起了手,當我叫他的時候他徑直走到了講台前,寫下了此問題的證明,自此之後我對馮諾依曼感到畏懼。)
Eugene Wigner(諾貝爾物理學獎獲得者):他很有幽默感,因他這種講故事和笑話的能力很受人即使是陌生人的喜愛,他可以在必要的時候變得簡單快樂,但絕不輕浮愚蠢。馮諾依曼這種非凡的大腦需要理解大部分像我們一樣的人不想去理解的甚至不奢求理解的東西。這個事實影響了馮諾依曼的道德判斷,只有在科學上的錯誤和不和諧的地方會讓他感到憤怒或者遺憾,在任何人犯了科學上面的錯誤時,他都會毫不猶豫地糾正別人的錯誤。
Herman Goldstine: 他的一個非凡的能力就是絕對精準的記憶力,據我所知,馮諾依曼有能力看過一本書或者一篇文章後一字不錯地背誦出來,更甚,他同樣能夠在多年以後不帶絲毫猶豫地做到。他還可以將其實時翻譯成英文背誦出來,而且速度絲毫不減。有一次我為了測試他的能力,問他《雙城記》是怎么開頭的,片刻,他開始背誦第一章節,直到可能10或者15分鐘後我讓他停下來。
成就評價 Miklós Rédei:It seems fair to say that if the influence of a scientist is interpreted broadly enough to include impact on fields beyond science proper, then John von Neumann was probably the most influential mathematician who ever lived.(如果論誰是在科學領域之間因為數學工作而輾轉,而每做一份工作都能在其領域套用數學並產生長遠的影響的,馮諾依曼可以說是有史以來最具有影響力的數學家。)
馮·諾依曼之墓 Glimm: he is regarded as one of the giants of modern mathematics.(他被普遍認為是現代數學的一位巨人。)
Jean Dieudonné: the last of the great mathematician.(最後一位傑出數學家。)
Peter Lax:20世紀最具科學頭腦的人。
 小時候的馮諾依曼
小時候的馮諾依曼 年輕時的馮·諾依曼
年輕時的馮·諾依曼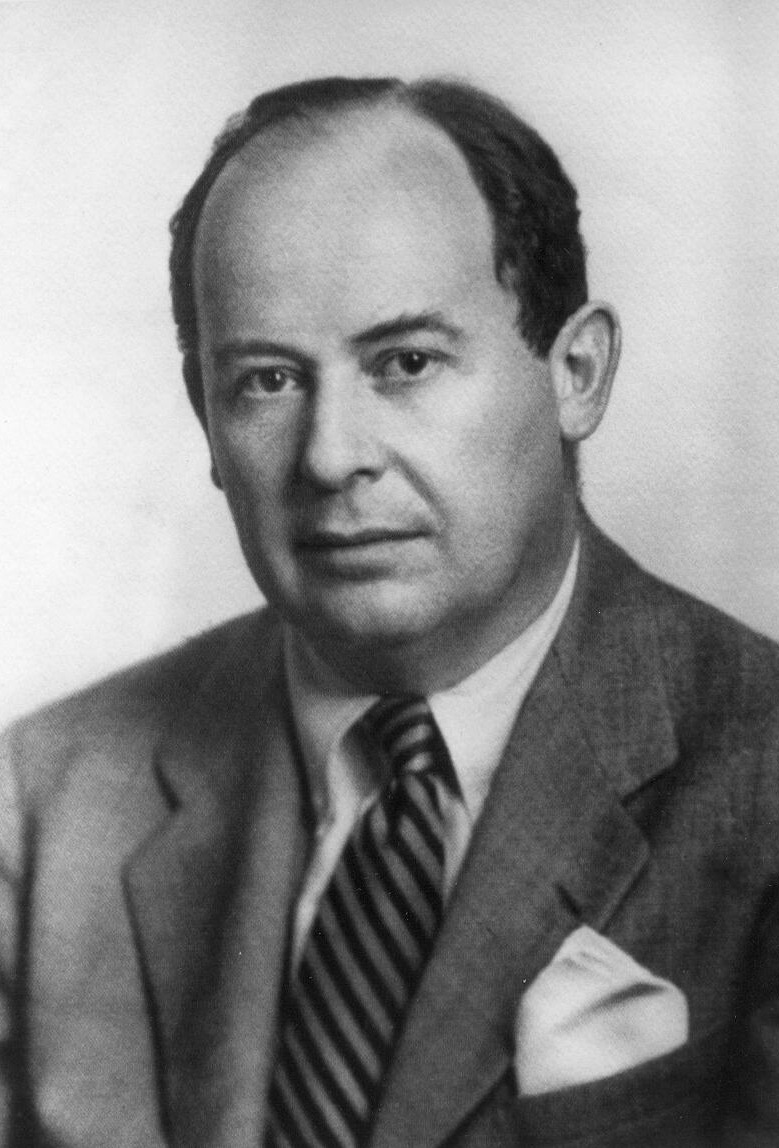 約翰·馮·諾依曼
約翰·馮·諾依曼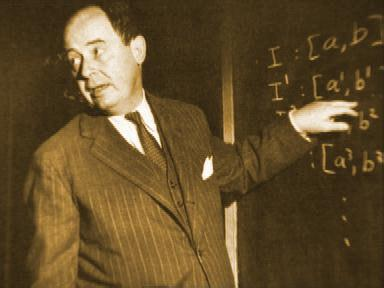 馮諾依曼在講課(“用黑板擦證明定理”)
馮諾依曼在講課(“用黑板擦證明定理”) 馮諾依曼和妻子克拉拉
馮諾依曼和妻子克拉拉 艾森豪為馮·諾依曼頒獎
艾森豪為馮·諾依曼頒獎
 馮·諾依曼和奧本海默在第一台計算機前合影
馮·諾依曼和奧本海默在第一台計算機前合影 馮諾依曼和摩根斯特恩
馮諾依曼和摩根斯特恩
 馮·諾依曼之墓
馮·諾依曼之墓
 馮·諾依曼(右)等在世界上第一台計算機前
馮·諾依曼(右)等在世界上第一台計算機前
