基本介紹
基本介紹
格
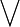
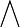
格中的運算律


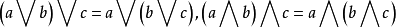
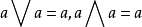
特殊的格



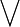



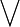
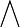


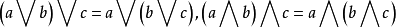
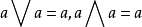



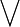



格論是抽象代數的分支,研究格的性質。一個格指的是其任意非空有限子集都有一個上確界(叫並)和一個下確界(叫交)的偏序集合(poset)。...
《一般格論基礎》作者:李海洋出版時間:2012-11...... 《一般格論基礎》系統地論述了一般格論的基本內容全書共分7章第1章介紹偏序集的基本知識;第2章闡述了半格...
“格”一種特殊的偏序集。在許多數學對象中,所考慮的元素之間具有某種順序。...... 偏序集和格就是研究順序的性質及作用而產生的概念和理論。格論在代數學、射影...
《現代數學基礎43:格論導引》講述格論的基本概念與基礎知識。其內容涵蓋:有序集、保序映射、格與半格、完全格、理想與同態、格同餘等基本概念;模格與半模格;...
對擴展的三段論的結論的2個項(s,p)前後分布的位置的不同排列構成擴展的三段論的結論格。擴展的三段論的結論格分為2個格。對於擴展的三段論的某一結論格,量詞排...
九型人格論把人格清晰簡潔的分成九種類型,每種類型都有其鮮明的人格特徵。九型人格論所描述的九種人格類型,並沒有好壞之別,只不過不同類型的人回應世界的方式具...
六君子格,四柱命理學術語,出自平派命理創建者邱平策先生所提出的“三局十格論”。...... 四柱命理學術語,出自平派命理創建者邱平策先生所提出的“三局十格論...
幾何格(geometric lattice)是一類重要的半模格。設L是格,若L既是半模格又是代數格,且L的每一緊緻元均是L的有限個原子的並,則稱L為幾何格。幾何格是有補格...
印綬格,印綬者,乃是生我之物。分正印和偏印(梟)區分。...... 印綬格分論 編輯 1、印綬主聰明,多智慧,性仁慈,語善良遲訥,體貌豐厚,能飲食,平生少病,不逢凶...
格密碼是一類備受關注的抗量子計算攻擊的公鑰密碼體制. 格密碼理論的研究涉及的密碼數學問題很多, 學科交叉特色明顯, 研究方法趨於多元化. 格密碼的發展大體分為兩...
“格”一種特殊的偏序集。在許多數學對象中,所考慮的元素之間具有某種順序。在數學中,完全格是在其中所有子集都有上確界(並)和下確界(交)的偏序集。完全格...
