預測控制模型

預測控制最初由Richalet和Cutler提出，它最大程度地迎合了工業過程控制的實際需求，控制綜合效果好。預測控制算法具有三大本質特徵：預測模型、滾動最佳化和反饋校正。代表性算法有：動態矩陣控制、模型算法控制、廣義預測控制和預測函式控制。

基本介紹

• 中文名：預測控制模型
• 外文名：Predictive control Model
• 提出者：Richalet和Cutler
• 三個步驟：預測模型;滾動最佳化;反饋校正
• 分為：線性模型;非線性模型
• 領域：自動控制

背景

20世紀70年代以來，隨著對工業過程控制要求不斷提高，人們力圖尋找對過程模型精度要求不高而同樣能實現高質量過程控制的方法。在這種需求背景下，預測控制逐漸發展起來。預測控制最初由Richalet和Cutler提出，它最大程度地迎合了工業過程控制的實際需求，控制綜合效果好，一經提出即在工業控制領域獲得了較快套用。隨著計算機技術的飛速發展，預測控制的套用領域也迅速擴展到包括航空、航天在內的眾多工程領域。

預測控制算法具有三大本質特徵：預測模型，滾動最佳化和反饋校正。它最大的特點是不斷滾動的局部最佳化，使模型失配、畸變、干擾等引起的不確定性及時得到彌補，從而得到較好的動態控制性能。正因如此，預測控制可推廣到有約束條件、大遲延、非最小相位以及非線性等過程，其強大的生命力受到控制界的極大關注。

預測控制技術發展至今，不僅在實際套用中取得了良好效果，而且在理論上也取得了突飛猛進的進展。最初的基於線性模型預測控制算法（MAC、DMC、GPC）已經相當成熟。近年來，非線性MPC（NLMPC）已成為預測控制研究的熱點，針對的研究對象是有擾動、有攝動和有約束的非線性過程控制。非線性 MPC 研究的困難主要體現在模型選取、能量函式求解和非線性算法等諸多方面。其中，非線性模型是非線性 MPC 的基礎，也是非線性 MPC區別於線性 MPC 的根本因素。

預測控制分類

（1）基於非參數模型的預測控制

代表性算法有：模型算法控制（MAC）、動態矩陣控制（DMC）。通常採用有限脈衝回響模型或有限階躍回響模型作為過程預測模型， 無須考慮模型結構和階次，模型中可包含過程純時滯項。其缺點是不能描述不穩定系統，不適用不穩定對象，線上模型辨識比較困難。

（2）基於滑動平均模型，即自適應模型的預測控制
主要代表算法廣義預測控制（GPC），融合自校正控制和預測控制的優點，其反饋校正以自校正的方式通過模型的線上辨識和控制規律的線上修正實現。優點是可用於開環不穩定、非最小相位和時變時滯等較難控制的對象，對系統的時滯和階次不確定等有良好的魯棒性，缺點是對於多變數系統，算法實現比較困難。

常用預測控制算法

常用的預測控制算法有：

（1）動態矩陣控制（Dynamic Matrix Control, DMC）

（2）模型算法控制（Model Algorithm Control, MAC）

（3）廣義預測控制(Generalized Predictive Control, GPC）

（4）預測函式控制（Predictive Functional Control, PFC）

預測控制基本原理

1978年， J.Richalet等就提出了預測控制算法的三要素：內部(預測)模型、參考軌跡、控制算法；現在則更清楚地表述為內部(預測)模型、滾動最佳化、反饋控制。

預測算法基本工作過程分為：模型預測、滾動最佳化、反饋校正。

(1)模型預測

預測模型旨在根據被控對象的歷史信息和未來輸入，預測系統未來回響。

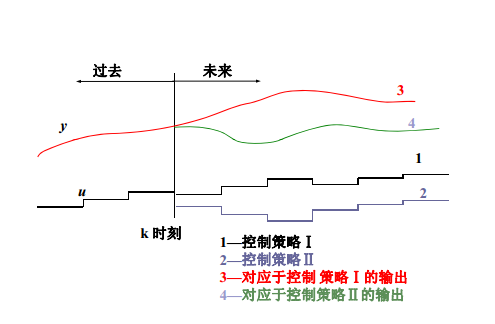圖1基於模型的預測示意圖

預測模型形式有①參數模型：如微分方程、傳遞函式、差分方程等；②非參數模型：如脈衝回響、階躍回響模型等。

(2)滾動最佳化

模型預測控制是一種最佳化控制算法，通過某一性能指標的最優來確定未來的控制作用。控制目的是通過某一性能指標的最優，確定未來的控制作用。其最佳化過程的特點：隨時間推移線上最佳化，反覆進行；每一步實現的是靜態最佳化；全局是動態最佳化

(3)反饋校正

模型預測控制是一種閉環控制算法。為了防止模型失配或環境干擾引起控制對理想狀態的偏離，預測控制通常不把這些控制作用逐一全部實施，而只是實現本時刻的控制作用。到下採樣時刻則需首先檢測對象的實際輸出，再通過實際測到的輸出信息對基於模型的預測輸出進行修正，然後再進行新的最佳化。不斷根據系統的實際輸出對預測輸出值作出修正使滾動最佳化不但基於模型，而且利用了反饋信息，構成閉環最佳化。

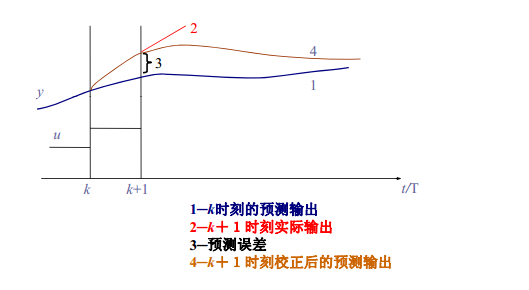圖2 誤差校正示意圖

反饋修正的形式有：在保持預測模型不變的基礎上，對未來的誤差做出預測並加以補償；根據線上辨識的原理直接修改預測模型。