基本介紹
基本介紹


















例題解析














用順序統計量估計參數
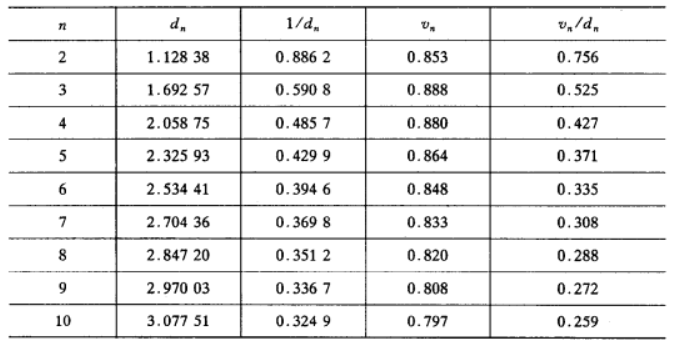
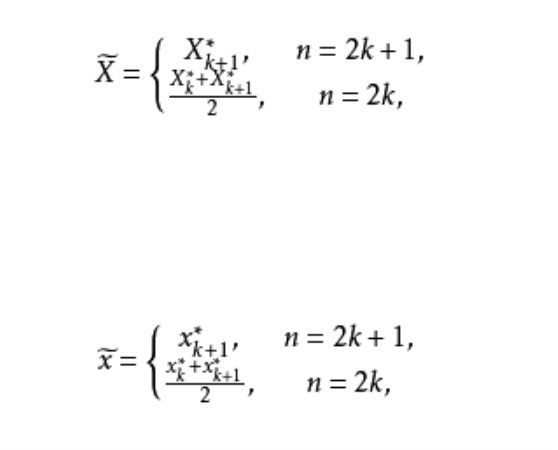

































順序統計量估計是指用順序統計量或其函式構造的估計。如,用極差估計標準差;用最小和最大觀測值估計均勻分布區間的兩個端點等。基本介紹順序統計量設是總體X的樣本,將它們自小到大排成,則這個排列稱為樣本順序統計量。抽取一個樣本,...
順序統計量,別稱是變數序列,亦稱變列分布函式。數理統計中的一種常用統計量。將樣本觀測值由小到大排列得到的統計量。定義 設 為總體 的樣本,記 為將 從小到大排列的第 個值,即對於任意基本事件 , 為將 從小到大...
(1) 最小順序統計量 (2)最大順序統計量 (3) 極差(Range)(4)四分位極差(iql)樣本X1,X2,…,Xn是獨立同分布的,而次序統計量X(1),X(2),…,X(n) 則既不獨立,分布也不相同。次序統計量的性質 次序統計量是充分統計量 證...
一、矩估計法 二、極大似然估計法 三、順序統計量估計法 第二節 估計量的評價標準 一、均方誤差 二、無偏性 三、有效性 四、一效性 第三節 充分性和完備性 一、充分性 二、完備性 三、指數族 第四節 區間估計 一、基本概念...
次序統計量和U 統計量在非參數統計中也有重要套用。前者可用於估計總體分布的分位數(見機率分布)、檢驗兩總體有相同的分布及構造連續總體分布的容忍限和容忍區間(見區間估計)等。後者主要用於構造總體分布的數字特徵的一致最小方差無偏...
統計學家已經發展了各種不同的穩健估計統計方法。三種較基本的精密估計類是:極大似然型估計(M估計)、順序統計量線性組合型估計類(L估計)和非參數型秩檢驗估計(R估計)。研究內容 精密估計應具備兩大特點:一是它能消除和削弱粗差對...
2.2 統計量 44 2.3 經驗分布函式、直方圖和順序 統計量 46 2.3.1 經驗分布函式 46 2.3.2 直方圖 48 2.3.3 順序統計量 50 2.4 數理統計中的某些常用分布 53 2.4.1 ?2分布 53 2.4.2 t分布 55 2.4.3 F分布 ...
第六章 參數估計 1 點估計 一、矩估計法 二、順序統計量法 三、極大似然估計法 習題6-1 2 估計量的評價標準 一、無偏性 二、有效性 三、一致性 習題6-2 3 區間估計 習題6-3 4 正態總體參數的區間估計 一、單個總體N( )...
2.3 統計量 2.3.1 樣本矩及其函式 2.3.2 順序統計量 2.4 經驗分布函式與直方圖 2.4.1 經驗分布函式 2.4.2 直方圖 2.5 抽樣分布 2.5.1 χ2分布 2.5.2 t分布 2.5.3 F分布 2.6 抽樣分布定理 2.6.1 單個正態...
2.4 順序統計量的分布 2.4.1 順序統計量的聯合分布 2.4.2 任何一個順序統計量的分布 2.4.3 任何兩個順序統計量的聯合分布 2.4.4 樣本極差的分布 習題二 第3章 參數估計理論 3.1 點估計 3.2 矩估計法 3.3 極...
2.5單組數據的位置參數置信區間估計 2.5.1順序統計量位置參數置信區間估計 2.5.2基於方差估計法的位置參數置信區間估計 2.6正態記分檢驗 2.7分布的一致性檢驗 2.7.1 X2擬合優度檢驗 2.7.2 Kolmogorov—Smirnov正態性檢驗 2....
3.3 隨機截尾情況下分布函式估計 3.3.1 殘存比率法計算產品的可靠度 3.3.2 平均秩次法計算經驗分布 3.4 順序統計量及相關套用 3.4.1 順序統計量的分布 3.4.2 樣本經驗分布函式的分布 3.4.3 各種截尾樣本的聯合...
第6章 數理統計的基本概念 154 6.1 知識要點 154 6.1.1 總體與樣本 154 6.1.2 統計量與抽樣分布 154 6.1.3 一些常用的統計量 154 6.1.4 經驗分布函式 154 *6.1.5 順序統計量 155 6.1.6 ? 2分布 155 6.1.7 ...
第2章數理統計的基本概念 29 2 1數理統計的一些基本概念29 2 2統計量和樣本矩31 2 2 1統計量的基本概念31 2 2 2樣本矩32 2 2 3順序統計量33 2 2 4經驗分布與格列汶科 定理35 2 3抽樣分布35 2 3 1正態總體樣本的線性...
樣本估計量的標準差反映了使用樣本數據來推斷總體參數時,統計量與總體參數真值之間誤差的平均水平。抽樣方法 順序抽樣 順序抽樣也稱機械抽樣或系統抽樣。按照某種既定的順序抽取一定數量的單位組成樣本,例如按總體各單位編號,或逢1或逢5...
第2章統計概念22 2.1數理統計的涵義22 2.2總體、樣本與統計量24 2.3順序統計量、經驗分布函式和直方圖27 2.4抽樣分布31 2.5套用案例37 習題238 第3章參數估計41 3.1點估計和區間估計的概念41 3.2矩估計和極大似然估計41 *...
系統統計量 系統統計量,由順序統計量的線性組合構的統計量。這一術語由莫斯泰勒(Mosteller)1946年引進。
§5.4 常用的統計量及其分布 1.統計量的定義 2.一個正態總體的常用統計量及其分布 3.兩個正態總體的常用統計量及其分布 4.非正態總體的均值的分布 5.順序統計量及其分布 習題5.4 第六章 總體分布中未知參數的估計 §6.1 ...
6.1.4統計量與抽樣分布 6.1.5一些常用的統計量 6.1.6經驗分布函式 *6.1.7順序統計量 6.1.8三大常用抽樣分布 6.1.9上α分位點 6.1.10正態總體的樣本均值與樣本方差的分布 6.1.11幾個常用結論 6.2典型例題分析 6.2....
順序統計量(Order Statistics)即它從小到大排列時的第 個值,常用於非參數估計與推斷中。常見的順序統計量包括樣本的最大值、最小值、中位數等。任給樣本 ,將其從小到大排成一列,記為:則其第一順序統計量(即最小值)為 ,...
譜窗估計是實際套用中的重要方法之一。譜分布F(λ)本身的一種相合估計可由I(ω)的積分直接獲得,即 。 研究以上各種估計量的統計性質,改進估計方法,是譜分析的重要內容。時域分析 它的目的在於確定序列在不同時刻取值的相互依賴關係...
