基本介紹
- 中文名:順序統計量
- 外文名:order statistic
- 別稱:變數序列、變列分布函式
- 所屬領域:數理統計
- 特點:將樣本觀測值由小到大排列
定義
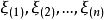

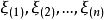
分布函式與分布密度




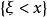






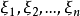


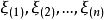


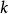
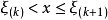
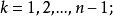



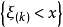



定理1





推論1
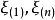


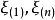


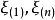
定理2
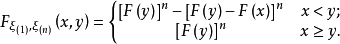



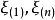
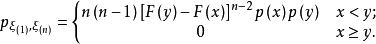
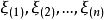

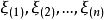




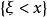






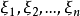


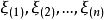


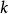
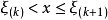
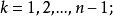



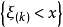








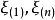


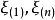


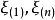
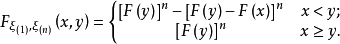



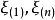
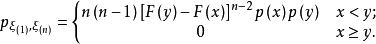
設X1,X2, …, Xn是取自總體X的樣本,X(i) 稱為該樣本的第i個次序統計量,它的取值是將樣本觀測值由小到大排列後得到的第i個觀測值。從小到大排序為x(1...
順序統計量,別稱是變數序列,亦稱變列分布函式。數理統計中的一種常用統計量。將樣本觀測值由小到大排列得到的統計量。...
順序統計量估計是指用順序統計量或其函式構造的估計。如,用極差估計標準差;用最小和最大觀測值估計均勻分布區間的兩個端點等。...
統計量是統計理論中用來對數據進行分析、檢驗的變數。巨觀量是大量微觀量的統計平均值,具有統計平均的意義,對於單個微觀粒子,巨觀量是沒有意義的.相對於微觀量的...
由順序統計量的線性組合構的統計量。這一術語由莫斯泰勒(Mosteller)1946年引進。 ...... 由順序統計量的線性組合構的統計量。這一術語由莫斯泰勒(Mosteller)1946年...
非參數方法有擬合優度檢驗、次序統計量、U統計量、秩統計量與秩方法、置換檢驗、非參數回歸與判別等等。非參數方法並非絕對只能解決非參數問題,有些也可用於典型的...
的列表中,對每一個從 1 到 k 的索引 i ,都有第 i 個元素與全排列後列表保持相同位置:偏排序後列表的第 i 個元素包含了輸入列表中的第 i 個順序統計量...
用求順序統計量問題最能說明“分治術” 算法設計思想,所謂順序統計問題是“從有n個元素的序列中選出第k個最小元素”,解此問題最容易想到的辦法是:將這n個元素...
夏皮羅一威爾克檢驗法5hapir}-W ilk lest一種檢驗正態性的方法,檢驗所使用的統計量:式中,i是將測定值由小到大順序排列時的次序,當,為偶數時,k‘uI2,當,...
Blum,Floyd,Prattle,Rivest和Tarjan給出了O(n)時間的求順序統計量的算法。隨後,Floyd和Rivest又在1973年對此作了改進。穩定的整序算法是Horvath在1974年提出的。大...
點估計(point estimation)是用樣本統計量來估計總體參數,因為樣本統計量為數軸上某一點值,估計的結果也以一個點的數值表示,所以稱為點估計。點估計和區間估計屬於...
