設 X1,X2, …, Xn是取自總體X的樣本,X(i) 稱為該樣本的第i個次序統計量,它的取值是將樣本觀測值由小到大排列後得到的第i個觀測值。從小到大排序為x(1),x(2), …,x(n),則稱X(1),X(2), …,X(n)為順序統計量。
基本介紹
- 中文名:次序統計量
- 外文名:Ordered Statistics
- 領域:數學
- 屬性:樣本觀測值由小到大排列的觀測值
- 性質:充分統計量
- 相關名詞:順序統計量
簡介



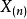


次序統計量的性質





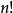
單個次序統計量的分布

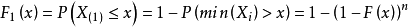

多個次序統計量的聯合分布
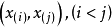

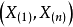


設 X1,X2, …, Xn是取自總體X的樣本,X(i) 稱為該樣本的第i個次序統計量,它的取值是將樣本觀測值由小到大排列後得到的第i個觀測值。從小到大排序為x(1),x(2), …,x(n),則稱X(1),X(2), …,X(n)為順序統計量。



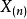







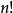

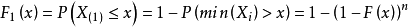

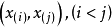

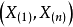


順序統計量,別稱是變數序列,亦稱變列分布函式。數理統計中的一種常用統計量。將樣本觀測值由小到大排列得到的統計量。...
設X1,X2, …, Xn是取自總體X的樣本,X(i) 稱為該樣本的第i個次序統計量,它的取值是將樣本觀測值由小到大排列後得到的第i個觀測值。從小到大排序為x(1...
順序統計量估計是指用順序統計量或其函式構造的估計。如,用極差估計標準差;用最小和最大觀測值估計均勻分布區間的兩個端點等。...
統計量是統計理論中用來對數據進行分析、檢驗的變數。巨觀量是大量微觀量的統計平均值,具有統計平均的意義,對於單個微觀粒子,巨觀量是沒有意義的.相對於微觀量的...
非參數方法有擬合優度檢驗、次序統計量、U統計量、秩統計量與秩方法、置換檢驗、非參數回歸與判別等等。非參數方法並非絕對只能解決非參數問題,有些也可用於典型的...
4.4 次序統計量4.4.1 次序統計量概念4.4.2 次序統計量的分布4.4.3 樣本極差4.4.4 樣本中位數與樣本p分位數4.4.5 五數概括及其箱線圖4.4.6 用隨機模擬法...
非參數統計法是當總體的具體分布函式形式未知且假設是關於分布本身而不是某些參數時,對這種類型的假設所做的推斷方法。該法利用所謂的次序統計量,就是按大小次序...
的列表中,對每一個從 1 到 k 的索引 i ,都有第 i 個元素與全排列後列表保持相同位置:偏排序後列表的第 i 個元素包含了輸入列表中的第 i 個順序統計量...
書主要講述了序言、導言、莖葉圖、字母值:一組當選的次序統計量、箱線圖和批比較、變換數據、y對x的耐抗線、用中位數分析雙向表、考查殘差、變換的數學方面、...
《套用機率統計》編委 (2006.11--至今)胡太忠研究方向 編輯 統計相依、隨機比較、可靠性理論、次序統計量、單調風險在國外雜誌Communications in Statistics: Theory ...
樣本的已知函式,其作用是把樣本中有關總體的信息匯集起來,是數理統計學中一個重要的基本概念。常用統計量有樣本矩、次序統計量、U統計量和秩統計量等。其中U統計...
用求順序統計量問題最能說明“分治術” 算法設計思想,所謂順序統計問題是“從有n個元素的序列中選出第k個最小元素”,解此問題最容易想到的辦法是:將這n個元素...
7.次序統計量的抽樣分布,《數學的理論與套用》(省級)2005年第3期;8.用差分方程計算行列式,《高等數學研究》(省級)2007年第1期。...
Blum,Floyd,Prattle,Rivest和Tarjan給出了O(n)時間的求順序統計量的算法。隨後,Floyd和Rivest又在1973年對此作了改進。穩定的整序算法是Horvath在1974年提出的。大...
統計量及其分布 1.2.1 統計量 1.2.2 常用的統計量 1.2.3 抽樣分布 1.2.4 來自正態總體的抽樣分布 1.3 次序統計量及其分布 1.3.1 次序統計量 1.3...
(t)是參數為λt的泊松分布隨機變數,而當X(t)=k已知的條件下,X的k個跳躍時刻與 k個在[0,t)上均勻分布且相互獨立的隨機變數的次序統計量(見統計量)有相同...
