鞍結分岔(saddle-node bifurcation)一種分岔類型,指控制參數變化過程中系統因形成鞍結點而出現的分岔。
基本介紹
- 中文名:鞍結分岔
- 外文名:saddle-node bifurcation

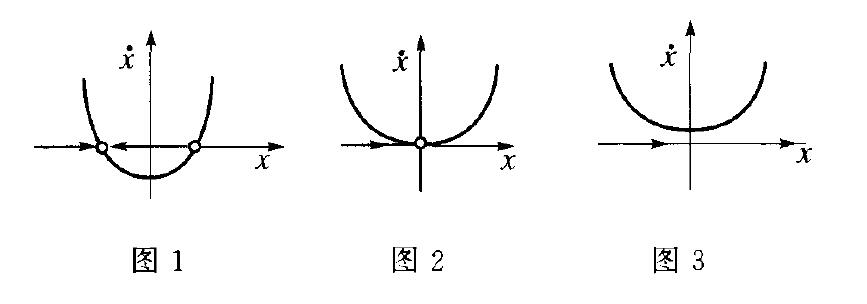
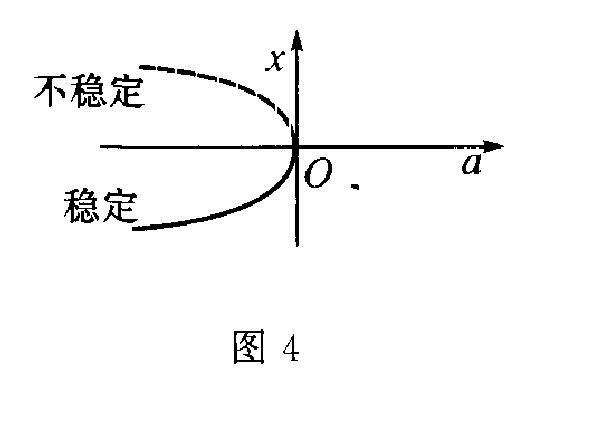
鞍結分岔(saddle-node bifurcation)一種分岔類型,指控制參數變化過程中系統因形成鞍結點而出現的分岔。



鞍結分岔(saddle-node bifurcation)一種分岔類型,指控制參數變化過程中系統因形成鞍結點而出現的分岔。鞍結分岔(saddle-node bifurcation)一種分岔類型,指控制參數變化過程中系統因...
鞍結分岔及霍普夫分岔是常見的局部分岔中,實際余維數為1的二個分岔(其他分岔的余維數都大於1)。不過跨臨界分岔及叉式分岔的正規式可以寫成只有一個參數的形式,因此也可以視為余維數為1的分岔。Bogdanov-Takens 分岔是一個有較多...
全書內容共分為9章,涉及不同周期激勵下分數階線性系統的共振分析,不同分數階非線性系統的叉形分岔、鞍結分岔、跨臨界分岔、分岔轉換以及分岔行為對共振現象的影響。本書採用待定係數法研究分數階線性系統的穩態回響,使求解過程大為簡化...
離散系統的分岔控制。消除系統的鞍結分岔、延遲跨臨界分岔;延遲、穩定Hopf分岔;控制擬周期分岔;控制系統的振幅、頻率、極限環等都是本項目的研究內容。通過參數設計來消除系統的有害的動力學行為,如跳躍、滯後現象,並使之產生有 ...
通過採用精確變換方法將非線性偏微分方程變換為非線性常微分方程,解決了一些無限維系統的求解和分岔控制問題;發現無限維系統也具有鞍結分岔、叉形分岔和跨臨界分岔三類典型的靜態分岔,利用反饋控制等方法研究了無限維系統的這幾類分岔的...
動力系統吸引域單重突變問題所研究的吸引域個數通常不超過三個,弧形結構振動系統存在眾多吸引域且具有眾多Wada域邊界結構或混雜拓撲邊界結構,申請者已發現該類型域邊界具有不同尋常的二重突變新現象,而吸引域邊界上的鞍結分岔和同宿正切...
如中心流形與範式理論和 Lyapunov-Schmidt 方法等. 在此基礎上,本書給出了動力系統中周期解與穩定性的確定過程,以及主要分岔問題的分析和計算方法,這些分岔包括鞍結分岔、音叉分岔、Hopf 分岔、Hopf-Hopf 分岔和Neimark-Sacker 分岔等...
(8)相平面數學分析表明交流外電場作用下細胞放電通過鞍結分岔或Hopf分岔產生動作電位;且外電場通過影響興奮性/抑制性離子電流的競爭機制,改變神經元放電的起始動態特性。
以豎向、轉動兩種彈性支撐邊界和模態之間1:1、1:2、1:3三種內共振形式為典型研究對象,得到了各種內共振的激發條件與不確定邊界條件之間的關係;獲取了各種外激勵下的幅值/頻率回響曲線,得到了鞍結分岔、Hopf分岔和倍周期分岔的參數域...
9.3 鞍結分岔 9.4 結論 參考文獻 第10章 超臨界軸向運動梁的分岔與振動 10.1 控制方程 10.2 數值方法 10.2.1 有限差分法 10.2.2 微分求積法 10.3 靜平衡位形及其分岔 10.3.1 靜平衡位形 10.3.2 分岔 10.4 耦合...
4.5分岔 4.5.1從液滴的旋轉穩定性談起 4.5.2分岔的主要類型 4.5.3不動點和線性化,不動點發生分岔的條件 4.5.4鞍結分岔及其在MEMS、肥皂膜、氣泡、膠體穩定性中的套用 4.5.5叉形分岔 4.5.6Hopf分岔 4.6混沌 4.6....
通過對含噪混合信號激勵下典型非線性系統的回響特性分析,研究了系統的分岔與動力學穩定性問題,得出了噪聲、時滯、阻尼等因素對隨機P分岔、Hopf分岔、叉形分岔、鞍結分岔、安全盆分岔等動力學現象的影響規律。在實驗研究方面,通過最大...
圖1和圖2分別給出了只出現轉子交叉耦合剛度項(即κ≠0)和只出現定子交叉耦合阻尼項(即γₛ≠0)時,參數平面(Ψ,β)上全周同頻碰摩解的穩定區域圖,圖1和圖2中的SN曲線表示同頻全周碰摩解的存在邊界(鞍結分岔邊界),曲線SNL...
在基於代表性單元流域水文模型通用框架基礎上,建立了具有較強物理機制的乾旱區河岸植被生態水文演化模型,在塔里木河流域開展了驗證和套用,並採用非線性數學方法揭示了生態水文耦合系統在一定條件下可以發生多重定態、鞍結分岔、混沌等非平凡...
包括雙參數空間的梳子狀混沌,具有“奇異”費根鮑姆常數的倍周期分岔的非光滑機制,識別了獨立於梳子狀混沌的新混沌,識別了隨機因素通過相干共振作用於I型興奮和鞍結分岔機制引起的新的隨機節律,以及位於新的加周期分岔序列內的非周期...
將量子系統及古典力學運動方程中分岔相連結的主要原因是在分岔時,古典力學軌道的signature會變大,正如Martin Gutzwiller在有關量子混沌中的研究所提出的一樣。許多分岔都研究來連結古典力學和量子力學,像是鞍結分岔、霍普夫分岔、umbilic...
並發現了小天體所有相對平衡點滿足的守恆量,指出了平衡點碰撞與湮滅過程中的多種可能的分叉類型,並在三小行星系統216 Kleopatra的平衡點碰撞湮滅過程中發現了鞍結分岔和鞍鞍分叉。
