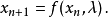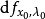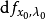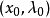分歧理論

分歧理論

分歧理論是研究在一帶參數的動力體系中平衡態隨參數變化時個數發生變化的現象，特別是平衡態由一個分裂為二個或多個的現象。近年來由於實際問題中不斷湧現出大量的分歧問題，也由於在理論上建立了較系統地處理這類問題的方法而發展成為一個獨立的數學研究方向。

分岔理論或分歧理論（bifurcation theory）是數學中研究一群曲線在本質或是拓撲結構上的改變。一群曲線可能是向量場內的積分曲線，也可能是一群類似微分方程的解。

基本介紹

  • 中文名：分歧理論
  • 外文名：bifurcation theory
  • 屬性：平衡態由一個分裂為二個
  • 研究：曲線在本質或是拓撲結構上的改變
  • 特徵：經常要討論分歧前後解的穩定性
  • 套用學科：數學
含義,分岔類型,局部分岔,全域分岔,分岔的余維數,套用,相關條目,

含義

分岔（bifurcation）常出現在動態系統的數學研究中，是指系統參數（分岔參數）小而連續的變化，結果造成系統本質或是拓撲結構的突然改變。分岔會出現在連續系統（以常微分方程、時滯微分方程或偏微分方程來描述）或是離散系統中 （以映射來描述）。
bifurcation一詞最早是由儒勒·昂利·龐加萊在1885年的論文中提出，這也是第一篇提到類似特性的數學論文，龐加萊後來也為許多不同的駐點命名而且分類。

分岔類型

分岔可以分為以下的二種類型：
  • 局部分岔（Local bifurcations）是指分岔特性可以用局部穩定性完全分析的分岔，一般會用參數通過臨界值時，平衡點、周期性軌跡或其他固定點的局部穩定性。
  • 全域分岔（Global bifurcations）是指分岔特性無法用局部穩定性完全分析的分岔，一般是指較大的不變集彼此重疊，或是和系統的平衡點重疊，這無法只靠平衡點的穩定性分析來求得。

局部分岔

局部分岔是指因參數變化，因此改變平衡點（或是不動點）穩定性的情形，對應平衡點特徵值的實部由正變負或是由負變正，在離散系統中（會由映射描述），是指不動點其弗洛凱乘子的模為1。這二種情形下，平衡點在分岔時都是非雙曲線的。
局部分岔有一個特性，只要控制分岔參數，可以將系統相圖中的拓樸變化限制在分岔點附近任意小的區域中，因此稱為局部分岔。
考慮用以下常微分方程描述的連續動態系統
若在
位置的雅可比矩陣有實部為0的特徵值，表示在此點有局部分岔。若特徵值為0，表示此分岔為穩態的分岔，但若特徵值為虛數，表示是霍普夫分岔。
若是離散系統
若在
的矩陣
有模數為1的特徵值，表示有局部分岔。若特徵值等於1，分岔可能是鞍結分岔、跨臨界分岔或叉式分岔，若特徵值等於-1，表示是周期加倍分岔，否則則為霍普夫分岔。
局部分岔的例子有：
  • 鞍結分岔（fold分岔）
  • 跨臨界分岔
  • 叉式分岔
  • 周期加倍分岔（flip分岔）
  • 霍普夫分岔
  • Neimark–Sacker分岔（二次霍普夫分岔）

全域分岔

全域分岔是指較大的不變集（如周期性軌跡）和平衡點重疊。全域分岔也會改變相圖上的拓樸，而且其變化不會像局部分岔一様限制在一個小區域，因此稱為全域分岔。
全域分岔的例子有：
  • 同宿分岔是指極限環和一個鞍點重疊。
  • 異宿分岔是指極限環和二個或多個鞍點重疊。
  • 無限周期分岔是指在極限環上有穩定節點和鞍點同時出現。
  • 藍天突變是指極限環和一個nonhyperbolic cycle重疊。
全域分岔有時會和像奇異吸引子之間更複雜的結構有關，如一種稱為危機的現象就是指當動態系統的參數變化時，奇異吸引子突然出現或是突然消失。

分岔的余維數

分岔的余維數是指動態系統中需變動幾個參數，才會使分岔現象出現。鞍結分岔及霍普夫分岔是常見的局部分岔中，實際余維數為1的二個分岔（其他分岔的余維數都大於1）。不過跨臨界分岔及叉式分岔的正規式可以寫成只有一個參數的形式，因此也可以視為余維數為1的分岔。
Bogdanov-Takens 分岔是一個有較多研究，余維數為2分岔的一個例子。

套用

分岔理論已用在連結量子系統及經典力學系統的動態中，可以用在原子系統、分子系統及諧振隧穿二極體。分岔理論已用到雷射動力學的研究中，也用在許多在實驗上難以處理的理論例子中，例如kicked top及耦合量子阱。將量子系統及古典力學運動方程中分岔相連結的主要原因是在分岔時，古典力學軌道的signature會變大，正如Martin Gutzwiller在有關量子混沌中的研究所提出的一樣。許多分岔都研究來連結古典力學和量子力學，像是鞍結分岔、霍普夫分岔、umbilic分岔、周期加倍分岔、重新連線分叉（reconnection bifurcation）、切線分叉（tangent bifurcation）及尖分叉（cusp bifurcation）。

相關條目

相關詞條

熱門詞條

聯絡我們