基本介紹
- 中文名:零導數定理
- 外文名:zero derivative theorem
- 適用範圍:數理科學
簡介
條件
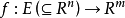
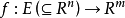
零導數定理是可微函式為常值函式的充分必要條件。若一元函式f在區間I上連續,在I的內部可微,則f為I上為常值函式的充分必要條件是f'=0。...
反之,已知導函式也可以倒過來求原來的函式,即不定積分。微積分基本定理說明了...(1)若導數大於零,則單調遞增;若導數小於零,則單調遞減;導數等於零為函式駐點,...
伯恩斯坦型定理即三角多項式逼近的逆定理,是由最佳逼近值收斂於零的速度刻畫函式的性質的定理。...
那么在(a,b) 內至少有一點ξ (a<ξ...
中值定理是反映函式與導數之間聯繫的重要定理,也是微積分學的理論基礎,在許多方面它都有重要的作用,在進行一些公式推導與定理證明中都有很多套用。中值定理是由眾多...
有理根定理是一個關於任意整係數方程的有理根的定理。在代數中,有理根定理(或有理根測試,有理零定理,有理零測試或p / q定理)表示對多項式方程的有理解與...
高斯-盧卡斯定理,又稱盧卡斯定理,該定理描述了復係數多項式的一個性質:多項式導數的根一定在原多項式的根所構成的凸包內。這一結論曾在1836被Carl Friedrich Gauss...
高斯一呂卡定理(Gauss-Lucas theorem)關於多項式零點位置的定理.該定理斷言:多項式Pm(z) 的導數的一切零點包含在Pm(z)的零點的凸包內....
在數學中,反函式定理給出了向量值函式在含有定義域中一點的開區域內具有反函式的充分條件。該定理還說明了反函式的全導數存在,並給出了一個公式。反函式定理可以...
施圖姆序列是把輾轉相除法套用於X和它的導數X1 = X′時,所得到的中間結果的...施圖姆定理表述 編輯 設σ(ξ)為以下序列中符號變化的次數(零不計算在內):...
關於位力定理的導出,可以將維里看作是系統慣量的時間導數,再進一步對維里求導得出,當然也需要證明,對穩定系統,慣量的二階時間導數平均值為0,過程也不算太麻煩。...
費馬(Fermat)引理是實分析中的一個定理,以皮埃爾·德·費馬命名。通過證明函式的每一個極值都是駐點(函式的導數在該點為零),該定理給出了一個求出可微函式的...
是無法求導數的。但此時有形式類近的斯托爾茲-切薩羅定理(Stolz-Cesàro theorem...在運用洛必達法則之前,首先要完成兩項任務:一是分子分母的極限是否都等於零(...
